信息安全数学基础-第五章-阶与原根

研究了二次剩余之后，研究n次剩余。研究阶和原根实际上是在研究这个剩余类加群元素的阶和生成元。

Overview

Abstract：

• 二次剩余/二次非剩余
• 勒让德符号
• 二次同余式

原根和二次剩余的关系：
1>原根一定是一个二次非剩余——因此，可以从二次非剩余中寻找最小原根。
2>素数p的原根g的奇数次幂分别与p的平方非剩余同余。
3>素数p的原根g的偶数次幂分别与p的平方剩余同余。

对上述结论的解释：
由上一章可以知道，二次同余这种关系将模m剩余类划分成了两个部分，其中，平方剩余的乘积还是平方剩余。而根据原根的定义，原根的幂次要生成模m剩余类中所有的元素，如果原根是一个二次剩余，那么原根的幂次就全是二次剩余，无法生成二次非剩余。因此，原根一定是一个二次剩余。
原根作为一个生成元，它的循环群中元素模m与模m剩余类中的元素一一对应，又知道，素数p的平方剩余和非平方剩余个数相同，可得上述结论。

重点梳理：

阶和原根的定义

阶的性质：

原根的性质：

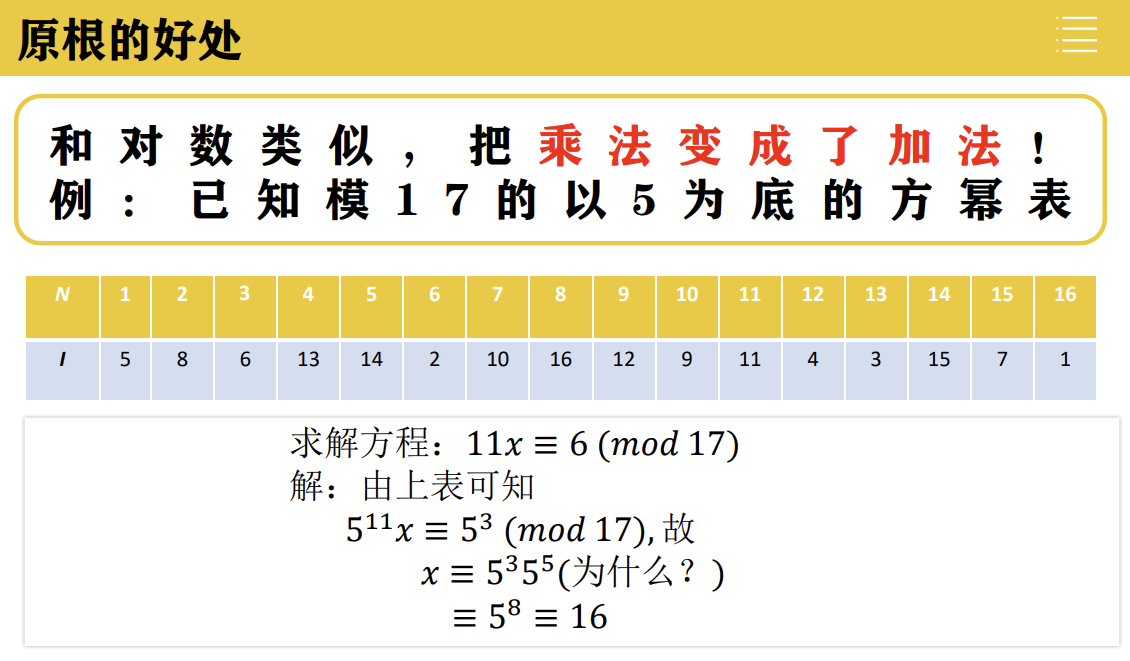
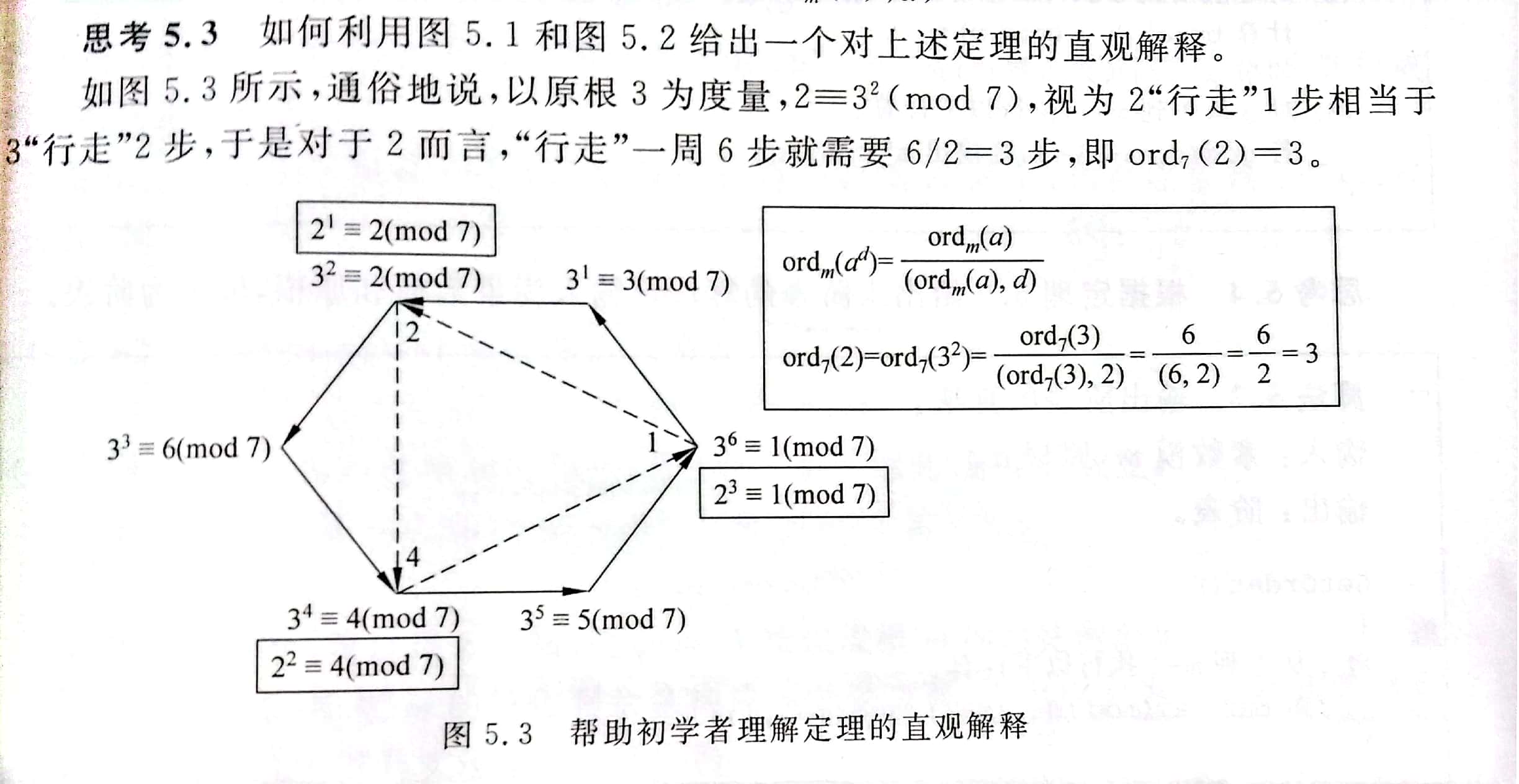
用生成元的角度更好理解这种关系，即让11再走几步等于3 =>8步
这种把乘法变成加法的规律实际上是因为原根g形成的循环群与整数模m同余类加法群同构。
这与群论中的性质相契合：任一循环群都能找到一个群与之同构。

原根的应用-密钥交换算法

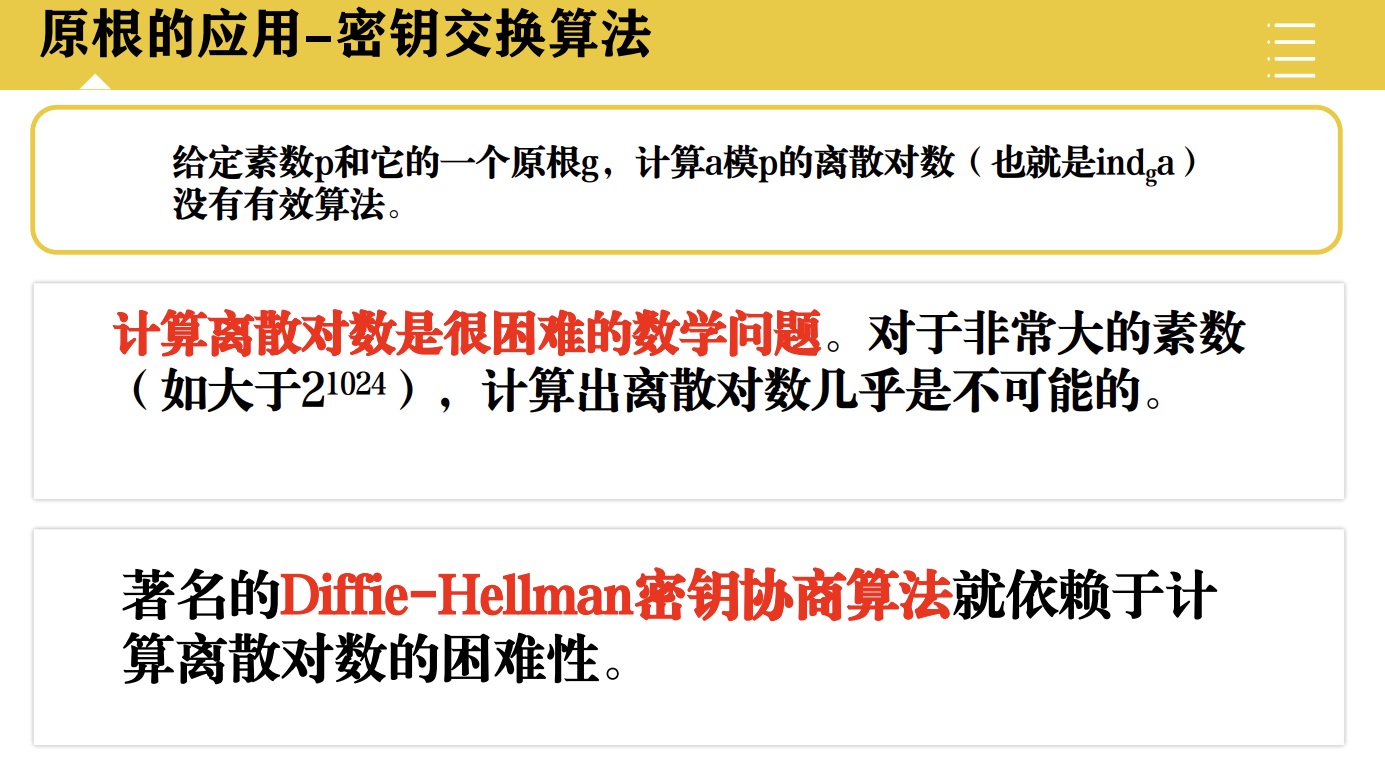
指数定理：

指数的应用-循环小数

考点归纳：

考点1：阶的判定，求阶

注意先化简，并在phi(m)中寻找阶。

考点2：阶的证明

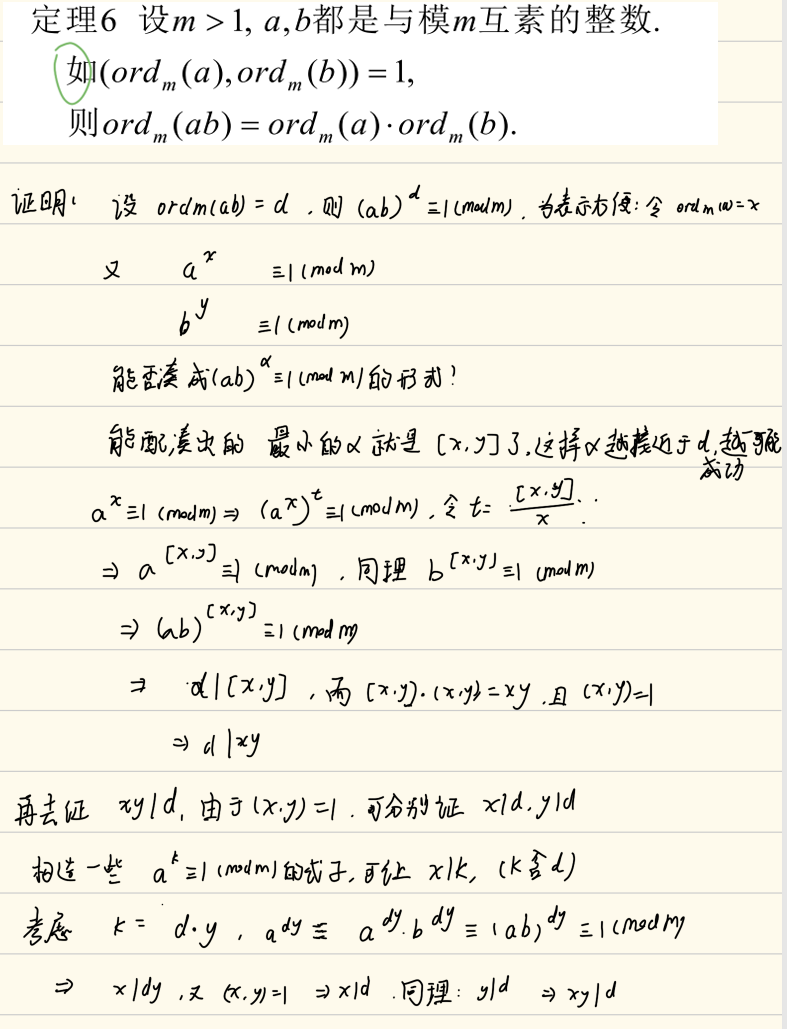
考点3：判断原根存在性

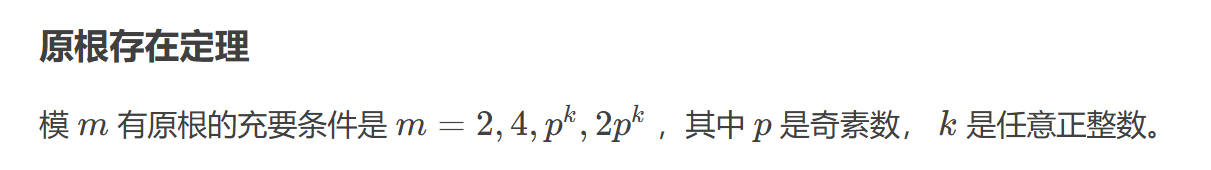
考点4：判断是否是原根

注：此处也可以联想二次剩余来解题，以判断2/3是否是47的原根为例：

小结论：

考点5：求最小原根

可对2-m-1逐个判断，也可在二次非剩余中逐个判断(更快)
实际上是判断是否是原根的问题，使用原根的充要条件如上。

考点6：求所有原根

由阶的基本性质可以推出：

考点7：原根的证明

考点8：求离散对数

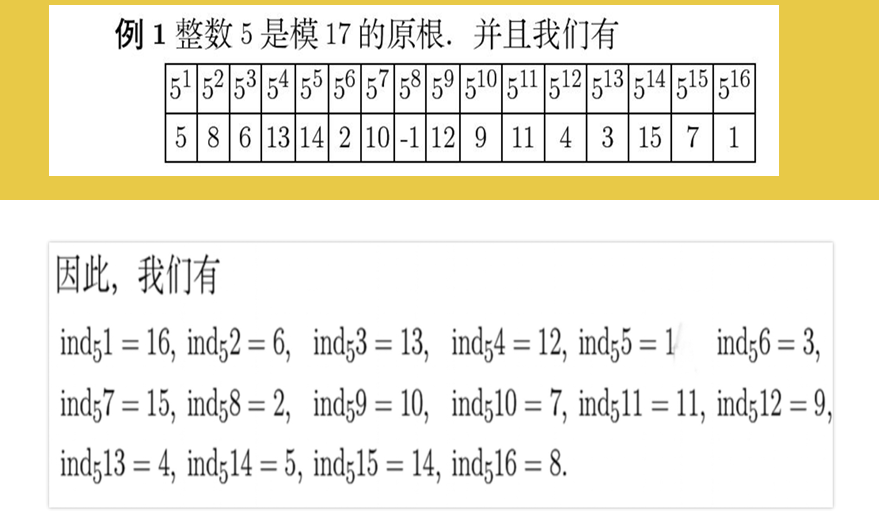
考点9：求解高次同余式

补充：

2的k次无原根
OI中计算原根
模板-原根
费马数的原根

ps：参考了复习课同学的pdf