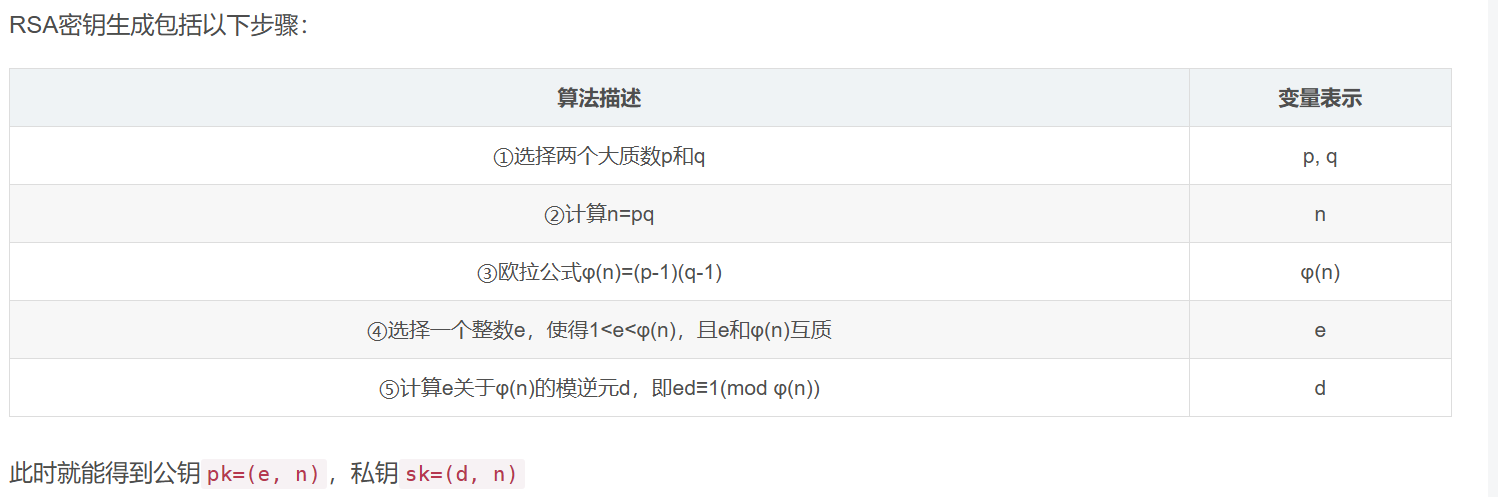
数论基础在密码学的应用举例
拿2024BaseCTF 的babyrsa举例:
题目 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 pythonfrom Crypto.Util.number import *b'BaseCTF{}' 1024 )65537 pow (m,e,n)print ("n =" ,n)print ("e =" ,e)print ("c =" ,c)""" n = 104183228088542215832586853960545770129432455017084922666863784677429101830081296092160577385504119992684465370064078111180392569428724567004127219404823572026223436862745730173139986492602477713885542326870467400963852118869315846751389455454901156056052615838896369328997848311481063843872424140860836988323 e = 65537 c = 82196463059676486575535008370915456813185183463924294571176174789532397479953946434034716719910791511862636560490018194366403813871056990901867869218620209108897605739690399997114809024111921392073218916312505618204406951839504667533298180440796183056408632017397568390899568498216649685642586091862054119832 """
单素数RSA是基于RSA算法的一个简化版本,其中使用的密钥只涉及一个素数。
在这题中,被加密的信息是字节数据m,为了对其进行加密,将m转换为大整数。
题解: 1 2 3 4 5 6 7 8 9 10 11 12 python
理解这个题解有两个个关键点:
欧拉函数的性质:若 p 为素数,则 ϕ ( p ) = p − 1 e × d = 1 m o d ( ϕ ( n ) ) \mathbf{欧拉函数的性质:若p为素数,则\phi(p)=p-1}\newline
\mathbf{e\times d=1\space mod(\space \phi(n))}\newline 欧拉函数的性质:若 p 为素数,则 ϕ ( p ) = p − 1 e × d = 1 mod ( ϕ ( n )) 已知 c = m e ( m o d n ) 如何反解 m ? 已知: a b ≡ a b ( m o d ϕ ( m ) ) ( m o d m ) ⟹ c ≡ m e ( m o d ϕ ( n ) ) ( m o d n ) 设整数 d , m ≡ c x ( m o d n ) ⟹ m e ( m o d ϕ ( n ) ) ≡ c x × e ( m o d ϕ ( m ) ) ≡ c 要使上式成立, d 必须满足是 e 在模 ϕ ( n ) 意义下的逆元,即 e × d = 1 m o d ( ϕ ( n ) ) \mathbf{已知c=m^e\space(mod\space n)如何反解m?}\newline
\mathbf{已知:a^b\equiv a^{b(mod\space\phi(m))} \space(mod \space m)}\newline
\mathbf{\implies c\equiv m^{e\space (mod \space \phi(n))}\space (mod \space n)}
\mathbf{设整数d,m\equiv c^x\space (mod \space n)}\newline
\mathbf{\implies m^{e\space (mod \space \phi(n))} \equiv c^{x\times e \space (mod\space \phi(m))} \equiv c}\newline
\mathbf{要使上式成立,d必须满足是e在模\phi(n)意义下的逆元,即e\times d=1\space mod(\space \phi(n))} 已知 c = m e ( mod n ) 如何反解 m ? 已知: a b ≡ a b ( mod ϕ ( m )) ( mod m ) ⟹ c ≡ m e ( mod ϕ ( n )) ( mod n ) 设整数 d , m ≡ c x ( mod n ) ⟹ m e ( mod ϕ ( n )) ≡ c x × e ( mod ϕ ( m )) ≡ c 要使上式成立, d 必须满足是 e 在模 ϕ ( n ) 意义下的逆元,即 e × d = 1 mod ( ϕ ( n )) 证明: a b ≡ a b ( m o d ϕ ( m ) ) ( m o d m ) 若 b < ϕ ( m ) :显然成立 若 b > = ϕ ( m ) : b = n ϕ ( m ) + k k = b ( m o d ( ϕ ( m ) ) ) a b ≡ a n ϕ ( m ) + k ≡ a n ϕ ( m ) × a k ( m o d m ) a ϕ ( m ) ≡ 1 ( m o d m ) [ 欧拉定理 ] a n ϕ ( m ) ≡ 1 ( m o d m ) ⟹ a b ≡ a k ( m o d m ) ⟹ a b ≡ a b ( m o d ϕ ( m ) ) ( m o d m ) \mathbf{证明:a^b\equiv a^{b(mod\space\phi(m))} \space(mod \space m)}\newline
\mathbf{若b<\phi(m):显然成立}\newline
\mathbf{若b>=\phi(m):}\newline
\mathbf{b=n\phi(m)+k}\newline
\mathbf{k=b(mod(\phi(m)))}\newline
\mathbf{a^b\equiv a^{n\phi(m)+k}\equiv a^{n\phi(m)}\times a^{k}\space (mod\space m)}\newline
\mathbf{a^{\phi(m)}\equiv1 \space (mod\space m) \space\space[欧拉定理]}\newline
\mathbf{a^{n\phi(m)}\equiv1 \space (mod\space m)}\newline
\mathbf{\implies a^{b}\equiv a^k\space (mod\space m)}\newline
\mathbf{\implies a^b\equiv a^{b(mod\space\phi(m))} \space(mod \space m)}\newline
\space \newline 证明: a b ≡ a b ( mod ϕ ( m )) ( mod m ) 若 b < ϕ ( m ) :显然成立 若 b >= ϕ ( m ) : b = n ϕ ( m ) + k k = b ( mod ( ϕ ( m ))) a b ≡ a n ϕ ( m ) + k ≡ a n ϕ ( m ) × a k ( mod m ) a ϕ ( m ) ≡ 1 ( mod m ) [ 欧拉定理 ] a n ϕ ( m ) ≡ 1 ( mod m ) ⟹ a b ≡ a k ( mod m ) ⟹ a b ≡ a b ( mod ϕ ( m )) ( mod m )