Algorithms-KMP
为了实现KMP算法,求出的nex数组会出现不同的情况。在我们的算法课中,认为旧教材中规定的nex数组是课程正确答案,而在有的同学的考研教辅中,nex数组不同。本文具体解释了这个问题,并给出了KMP的编程实现。
nex数组是什么?
概括地说,nex数组就是针对模式串p生成的一个数组,记录了公共前后缀长度——border长度,这个信息会被用来完成KMP算法中的回溯步骤,讲字符串匹配算法的时间复杂度降到O(n)
不同版本的nex数组差异在哪里?
- 旧版本:nex[0]一定等于0
- 新版本:nex[0]一定等于0
- 其它情况:旧版nex[i]=新版nex[i]-1
笔算做题时要注意这种问题,旧版本的nex数组是不会有连续的0出现的,nex[i]=匹配串的最大公共前后缀 + 1
为什么会出现这样的差异?
这里我认为是因为在KMP算法实现中对特殊情况的不同处理办法,下面是旧版中next[j]的定义:
可以发现,当j=1时,nex[j]被强行规定为0,这时为了完成后续的KMP算法,0被赋予了特殊的含义——第一个字符就失配,此时如果回溯到下标为0的地方就会出错,因为在课程教材中,字符串的下标是从1开始的,下标为0的地方存储的是字符串长度。
但是,如果此时回溯到下标为1的地方,就会陷入死循环
为什么会陷入死循环?
我们知道,在KMP算法中,要匹配的字符串s的下标指针i是不会倒退的,那这时如果第一个字符匹配失败还讲j回溯到下标1(当前就在下标1),就会重复这个比较过程一直循环。
这就启发这里的算法实现必须对nex[1]进行特殊处理。书中的KMP实现如下:
求nex数组(求border)
不同的KMP代码实现对应了不同的nex数组,同时也对应了不同的数组下标使用方式。原理相同,但是不可混用。
教材规定的KMP的nex数组实现:

1
2
3
4
5
6
7
8
9
//另一种
nex[0]=nex[1]=0;//初始化
for(int i=2,j=0;i<=m;i++)
{
while(j&&p[i]!=p[j+1]) j=nex[j];
if(p[i]==p[j+1]) j++;
nex[i]=j;
}
//如果采用这种办法,后续的KMP匹配过程就换用for循环嵌套while循环,对于回溯到nex[j]=0的情况,即使第一个就失配,i还是会++,同样也避免了死循环。
1 | |
KMP算法模板(C++)
1 | |
2025/1/1:
上述问题其实我没有弄清楚,直到昨天听了数据结构的期末复习讲解。引用ppt,感觉这个解释清楚了。
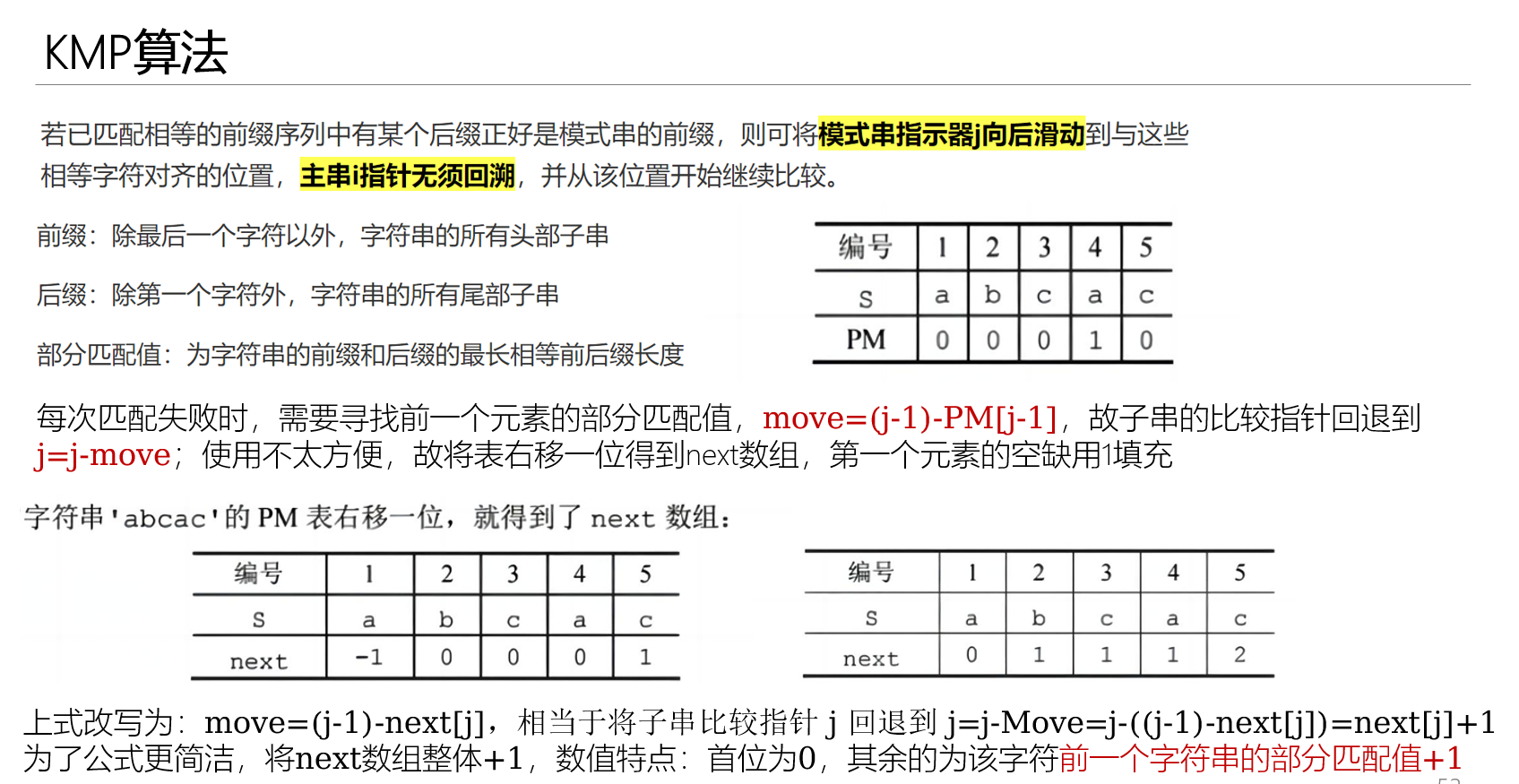
KMP 的时间复杂度分析

Algorithms-KMP
https://43.242.201.154/2024/11/23/Algorithms-KMP/