数理逻辑-集合与逻辑-逻辑代数

几乎是同时地，概率统计、数字电路基础、离散数学三门核心课同时涉及到了非常类似的内容。所以这篇blog作为总序，希望可以阐明这其中的区别与联系，为三门课程的后续打下个好基础。另外就是在这里集中整理一下De Morgan律的证明与应用（因为到处在用）。

开宗明义：为什么有那么多这么相似的符号，什么时候成了逻辑语句，什么时候又成了集合？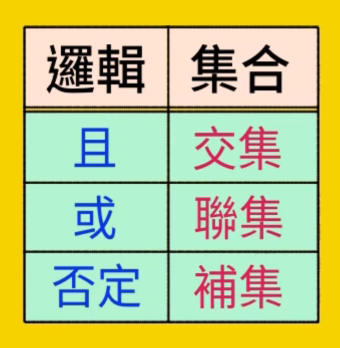

简言之，数电和离散数学（第一二章）在用逻辑解决问题，而概统和离散数学（第三章）在用集合解决问题。而集合与逻辑的关系如上图。
“一阶逻辑的语法、语义概念都可以在集合论中定义， 关于一阶逻辑的定理可以被看作是集合论的定理”。

概率统计：

事件为集合，事件间的关系和运算按照集合间的关系和运算来处理。由“事件发生”的含义，当赋予集合间的关系和运算以概率含义时，就得到事件间的关系和运算.

电子技术基础（数字部分）：

逻辑代数有一定的定理、定理和规则，用它们对数学表达式进行处理，可以完成对逻辑电路的化简、变换、分析和设计。
利用逻辑代数这种数学工具，可以把逻辑电路输入和输出之间的关系用代数方程表示出来。

离散数学：

命题逻辑：命题是逻辑学研究的出发点。
一阶谓词逻辑：命题逻辑的不足，在于它不能有效区分主体客体。
集合与关系：集合是数学中最为基本的概念，又是数学各分支等各领域最普遍的描述工具。

De Morgan定律

同一个东西，离散数学里叫De Morgan律，数电中叫反演规则，概统叫对偶律。应用很多，可以说是三门共同的考点。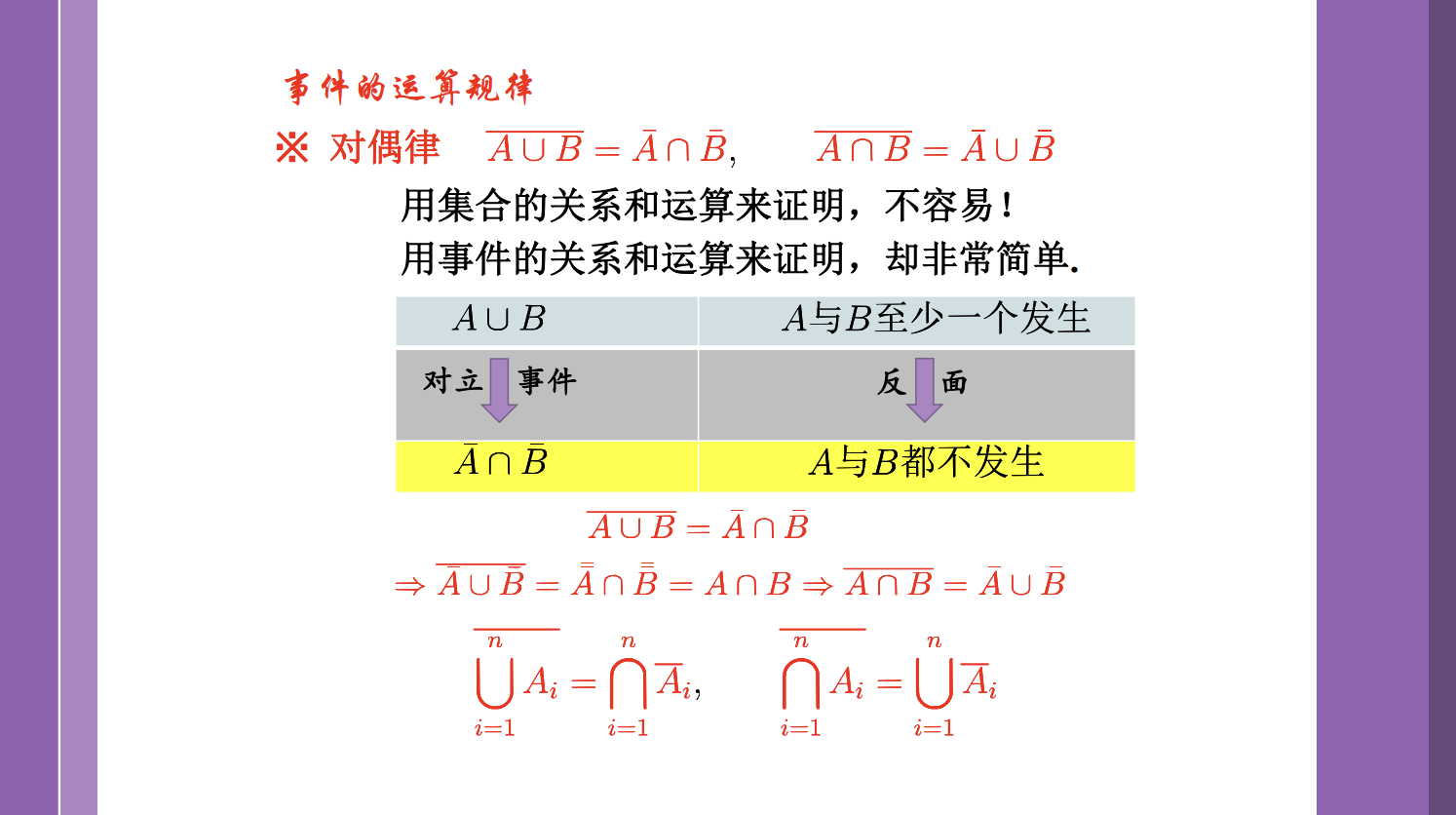


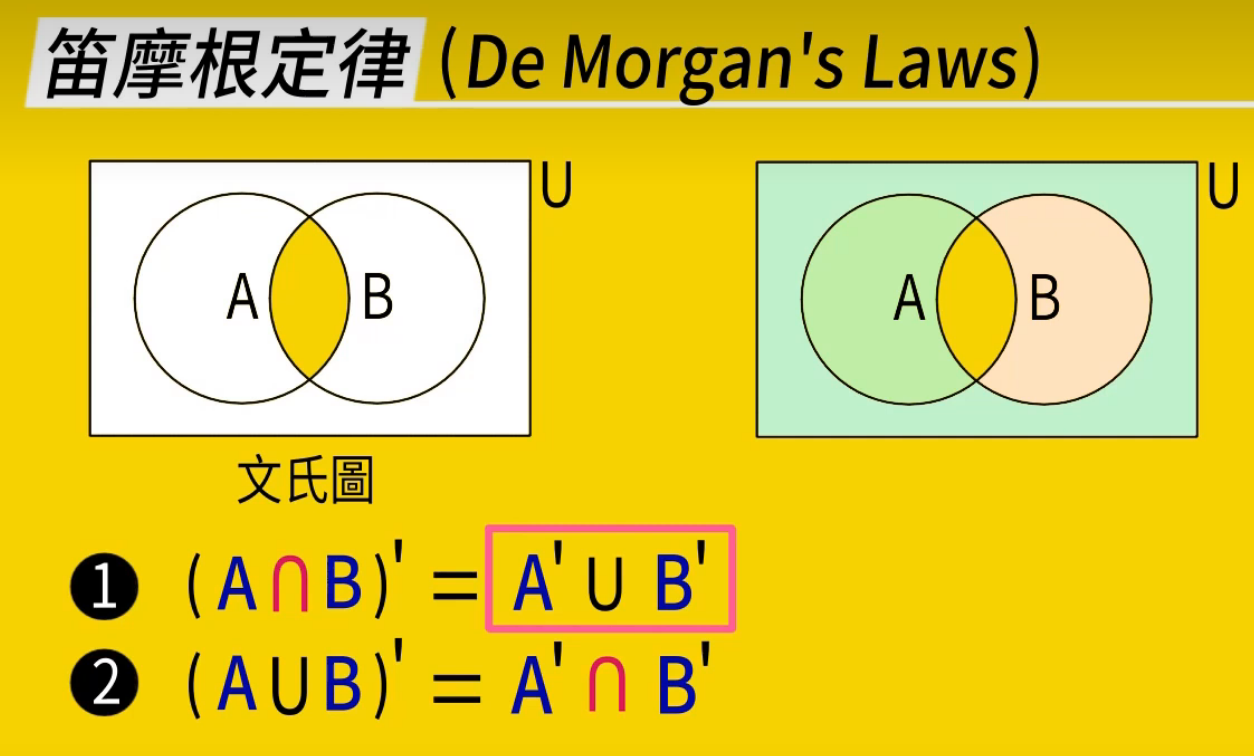
直接用数学语言证明不太容易，以上两种办法即可。但是更重要的还是其应用。