Datastructures-树(上)

后来才明白，为什么非要有树这种东西。
树的遍历，前序、中序、后序、层序，非递归，递归

引入：二分查找

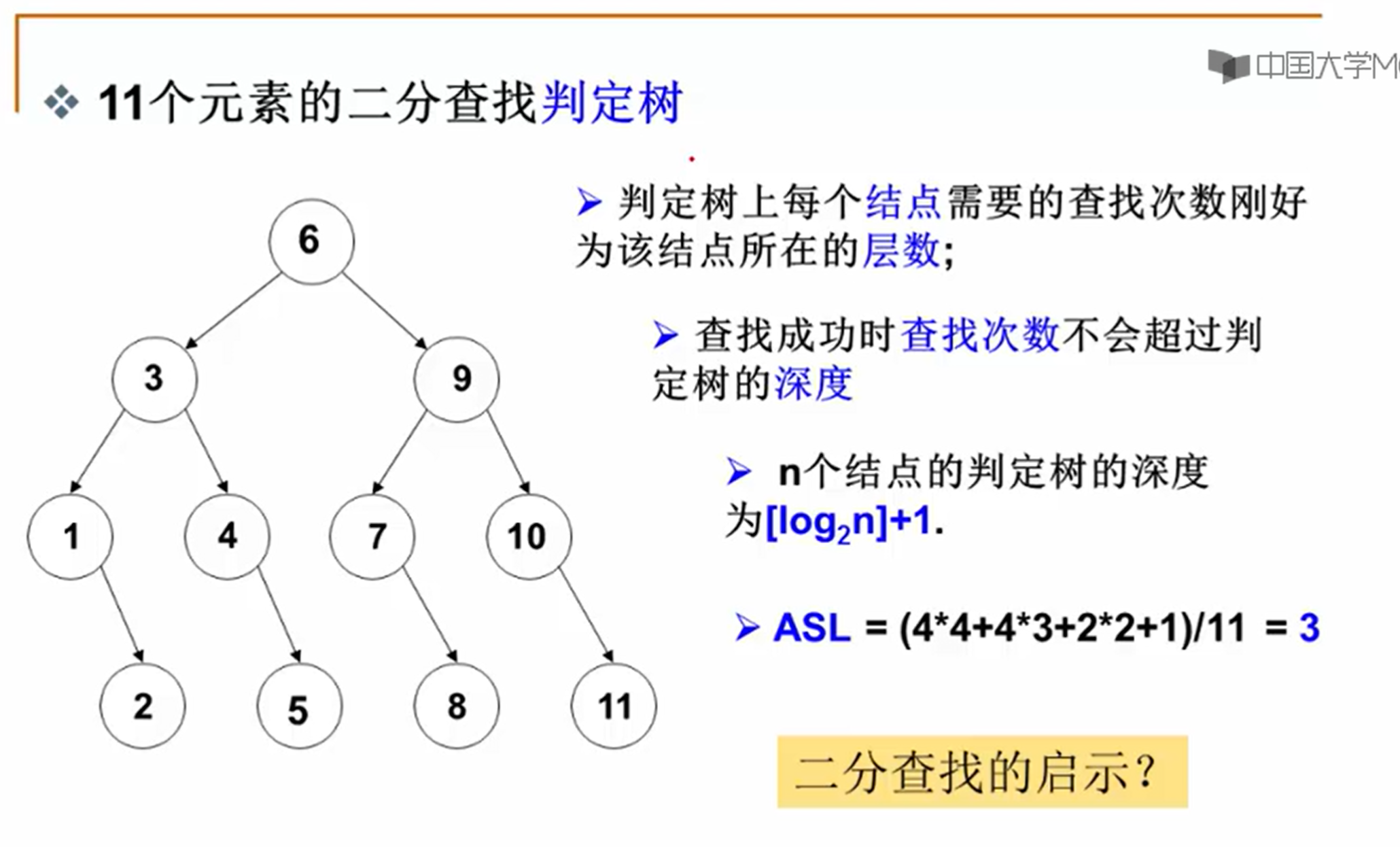
“从这里面我们可以看到，由于我们在数组里面，对于我们要查找的元素，进行了有序化的一种组织，使得我们的查找过程是按照固定的顺序，或者说，是按照事先定义好的顺序来进行的。”
而这个顺序呢，是形成我们所说的类似树这样的一个结构

那反过来说，能不能把数据不一定放在数组？
我就按照这样的一个层次化的结构来存放数据，是不是也会达到二分查找一样的效果？”

这就顺理成章地引入了树这种数据结构，用树的结构存储数据。
使得插入、查找、删除等等操作更加方便。
这样一来，动态查找问题也得到了解决！

树的定义

……

树的表示

Q:每个结点设计几个指针域呢？事先不知道它有几个子节点，那怎么办？
A:每个结点都留5个吧，这就能存下了，但是造成了大量的空间浪费。
A:儿子-兄弟表示法，只用两个指针域！

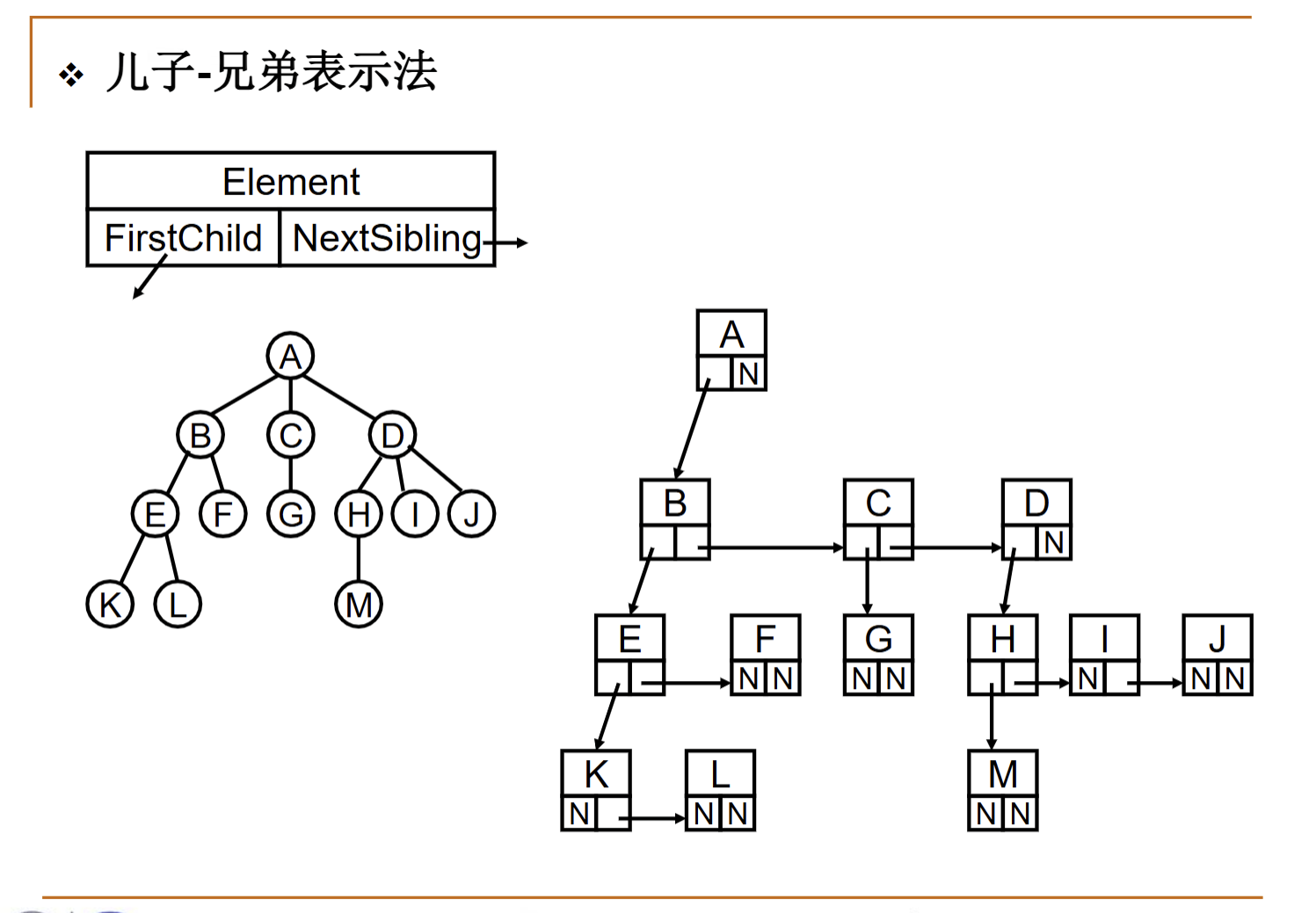
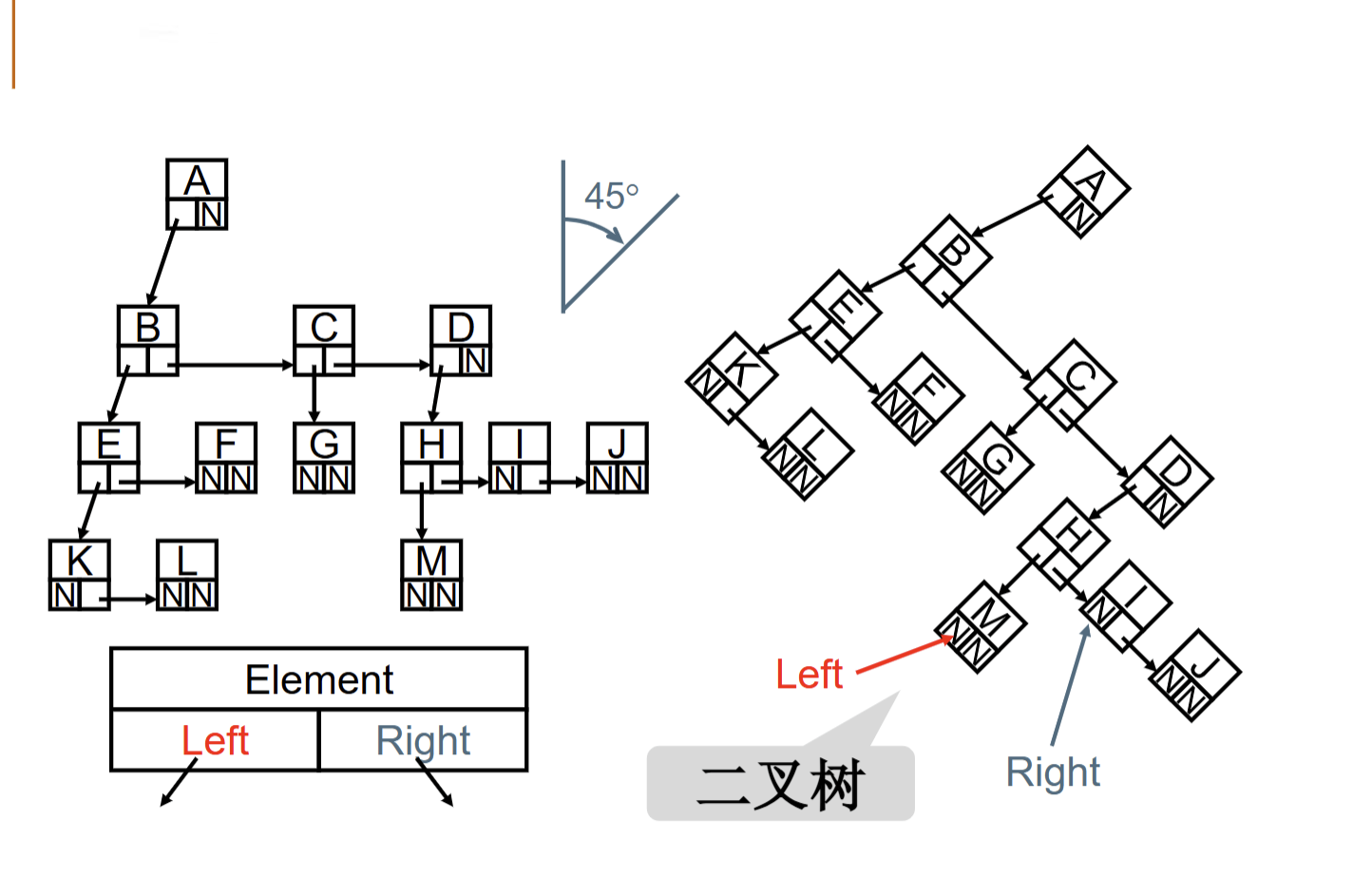
PS：儿子兄弟表示法如何实现呢？

• 1.链式前向星，即数组模拟链表
• 2.邻接矩阵，用C++的二维向量实现
• 3.真链表

▶

BT

#include<stdio.h>
#include<malloc.h> 
#include<vector> 
#include<queue>
#include<algorithm>
typedef struct TreeNode *BinTree;
struct TreeNode{
	int Data;  // 存值 
	BinTree Left;    // 左儿子结点 
	BinTree Right;   // 右儿子结点 
};
BinTree CreatBinTree();   // 创建一个二叉树
bool IsEmpty(BinTree BT);  // 判断树 BT 是否为空 
void PreOrderTraversal(BinTree BT);   // 先序遍历，根左右
void InOrderTraversal(BinTree BT);    // 中序遍历，左根右 
void PostOrderTraversal(BinTree BT);  // 后序遍历，左右根 
using namespace std;
typedef struct SNode *Stack;
struct SNode{
	BinTree Data;
	Stack Next;
};


Stack CreateStack();  // 初始化链栈 
int IsEmpty(Stack S);  // 判断链栈是否为空 
void Push(Stack S,BinTree item);  // 入栈 
BinTree Pop(Stack S);  // 出栈
 

// 初始化 
Stack CreateStack(){
	Stack S;
	S = (Stack)malloc(sizeof(struct SNode));
	S->Next = NULL;
	return S;
}

// 判断是否为空 
int IsEmpty(Stack S){
	return (S->Next == NULL);
}

// 入栈
void Push(Stack S,BinTree item){
	Stack tmp;
	tmp = (Stack)malloc(sizeof(struct SNode));
	tmp->Data = item;
	// 链栈栈顶元素是链表头结点，新入栈的链表在栈顶元素后面 
	tmp->Next = S->Next;   
	S->Next = tmp;
} 

// 出栈
BinTree Pop(Stack S){
	Stack First;
	BinTree TopVal;
	if(IsEmpty(S)){
		printf("堆栈空");
		return 0;
	}else{
		First = S->Next;   // 出栈第一个元素在栈顶元素后面 
		S->Next = First->Next;  //把第一个元素从链栈删除 
		TopVal = First->Data;   // 取出被删除结点的值 
		free(First);  // 释放空间 
		return TopVal;
	}
} 

BinTree Insert(int Data){
	BinTree BT;
	BT =  (BinTree)malloc(sizeof(struct TreeNode));
	BT->Data = Data;
	BT->Left = NULL;
	BT->Right = NULL;
	return BT;
}

// 初始化二叉树 
BinTree CreatBinTree(){
	BinTree BT;
	BT =  (BinTree)malloc(sizeof(struct TreeNode));
	BT->Data = 1;
	BT->Left = Insert(2);
	BT->Right = Insert(3);
	BT->Left->Left = Insert(4);
	BT->Left->Right = Insert(6);
	BT->Left->Right->Left = Insert(5);
	BT->Right->Left = Insert(7);
	BT->Right->Right = Insert(9);
	BT->Right->Left->Right = Insert(8);
	return BT;
}


// 判断树是否为空
/*bool  IsEmpty(BinTree BT){
}*/

// 先序
/*void  PreOrderTraversal(BinTree BT){
	if(BT){
		printf("%d",BT->Data);  // 打印根 
		PreOrderTraversal(BT->Left);  // 进入左子树 
		PreOrderTraversal(BT->Right);  // 进入右子树 
	}
} */

// 先序非递归 
void PreOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while(T || !IsEmpty(S)){  // 当树不为空或堆栈不空 
		while(T){     
			Push(S,T);    // 压栈，第一次遇到该结点 
			printf("%d",T->Data);  // 访问结点
			T = T->Left;   // 遍历左子树 
		}
		if(!IsEmpty(S)){  // 当堆栈不空 
			T = Pop(S);    // 出栈，第二次遇到该结点 
			T = T->Right;  // 访问右结点 
		}
	} 
} 

// 中序递归 
/*void InOrderTraversal(BinTree BT){
	if(BT){
		InOrderTraversal(BT->Left);  // 进入左子树 
		printf("%d",BT->Data);  // 打印根 
		InOrderTraversal(BT->Right);  // 进入右子树 
	} 
} */

// 中序非递归
void InOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while(T || !IsEmpty(S)){  // 当树不为空或堆栈不空 
		while(T){     
			Push(S,T);    // 压栈
			T = T->Left;   // 遍历左子树 
		}
		if(!IsEmpty(S)){  // 当堆栈不空 
			T = Pop(S);    // 出栈
			printf("%d",T->Data);  // 访问结点
			T = T->Right;  // 访问右结点 
		}
	} 
} 

// 后序
/*void PostOrderTraversal(BinTree BT){
	if(BT){
		PostOrderTraversal(BT->Left);  // 进入左子树 
		PostOrderTraversal(BT->Right);  // 进入右子树 
		printf("%d",BT->Data);  // 打印根 
	} 
} */ 

// 后序遍历 
void PostOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	vector<BinTree> v;
	Push(S,T);
	while(!IsEmpty(S)){  // 当树不为空或堆栈不空 
		T = Pop(S);
		v.push_back(T);
		if(T->Left)
			Push(S,T->Left);
		if(T->Right)
			Push(S,T->Right);
	}
	reverse(v.begin(),v.end());  // 逆转 
	for(int i=0;i<v.size();i++)
		printf("%d",v[i]->Data);
} 
/*
  void PostOrderTraversal(Bintree BT) {  //给节点增加访问次数的属性Visit，初始化为0
  Bintree T BT;
  Stack S = CreateStack(Maxsize);
  while (T || !IsEmpty(S)) {
  while (T) {
  if (T->Visit == 0) {//虽然没必要判断，为便于理解
  T->Visit++;
  Push(S, T);  //第一次入栈，不访问
  }
  T = T->left;   //转向左子树
  }
  if (!IsEmpty(S)) {
  T = Pop(s);
  if (T->Visit == 2)    {
  printf("%d", T->Data);//第三次碰到它，访问节点，可以彻底从堆栈弹出了
  T = NULL;//左右子数均已经访问过
  }
  else {
  T->Visit++;
  Push(S, T);  //第二次入栈，不访问，（相当于T没有出栈）
  T = T->Right;  //转向右子树
  }
  }
  }
 */

// 层次遍历
void LevelOrderTraversal(BinTree BT){
	queue<BinTree> q;
	BinTree T;
	if(!BT)
		return;
	q.push(BT);  // BT 入队 
	while(!q.empty()){
		T = q.front();  // 访问队首元素 
		q.pop();  // 出队
		printf("%d",T->Data);
		if(T->Left)
			q.push(T->Left);
	 	if(T->Right)
	 		q.push(T->Right);
	}
}
// 输出叶子结点
void  FindLeaves(BinTree BT){
	if(BT){
		if( !BT->Left && !BT->Right)
			printf("%d",BT->Data);  // 打印叶子结点
		FindLeaves(BT->Left);  // 进入左子树 
		FindLeaves(BT->Right);  // 进入右子树 
	}
} 

// 求树高度
int  GetHeight(BinTree BT){
	int hl,hr,maxh;
	if(BT){
		hl = GetHeight(BT->Left);  // 求左子树高度 
		hr = GetHeight(BT->Right);  // 求右子树高度 
		maxh = (hl>hr)?hl:hr;
		return maxh+1;  // 当前结点高度为左右子树最大的高度+1 
	}else
		return 0;
} 
int main(){
	BinTree BT,ST;
	BT = CreatBinTree();
	printf("先序遍历：");
	PreOrderTraversal(BT);
	printf("\n中序遍历：");
	InOrderTraversal(BT);
	printf("\n后序遍历：");
	PostOrderTraversal(BT);
	printf("\n层次遍历：");
	LevelOrderTraversal(BT);
	printf("\n输出叶子结点:"); 
	FindLeaves(BT);
	printf("\n输出树的高度：%d",GetHeight(BT));
	return 0;
}