数据结构与算法

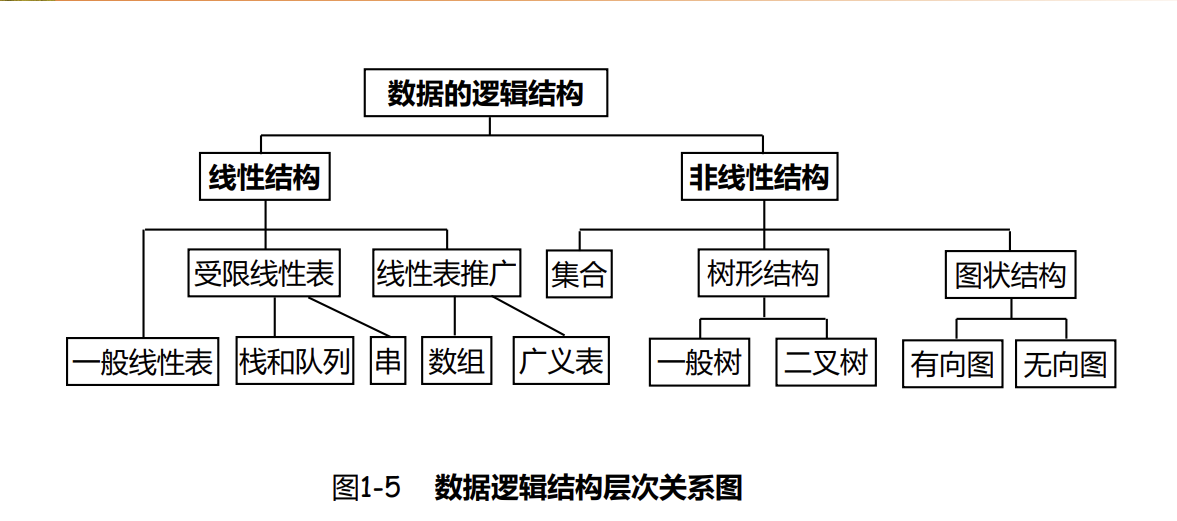
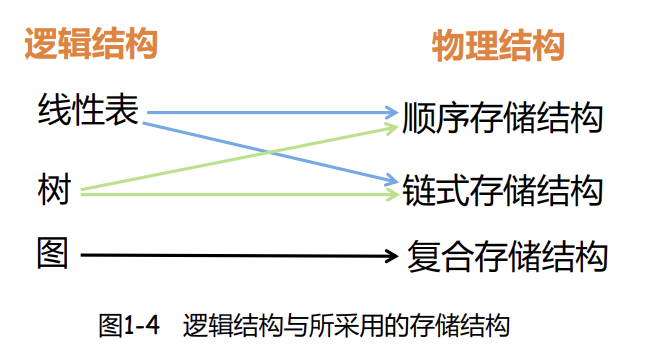
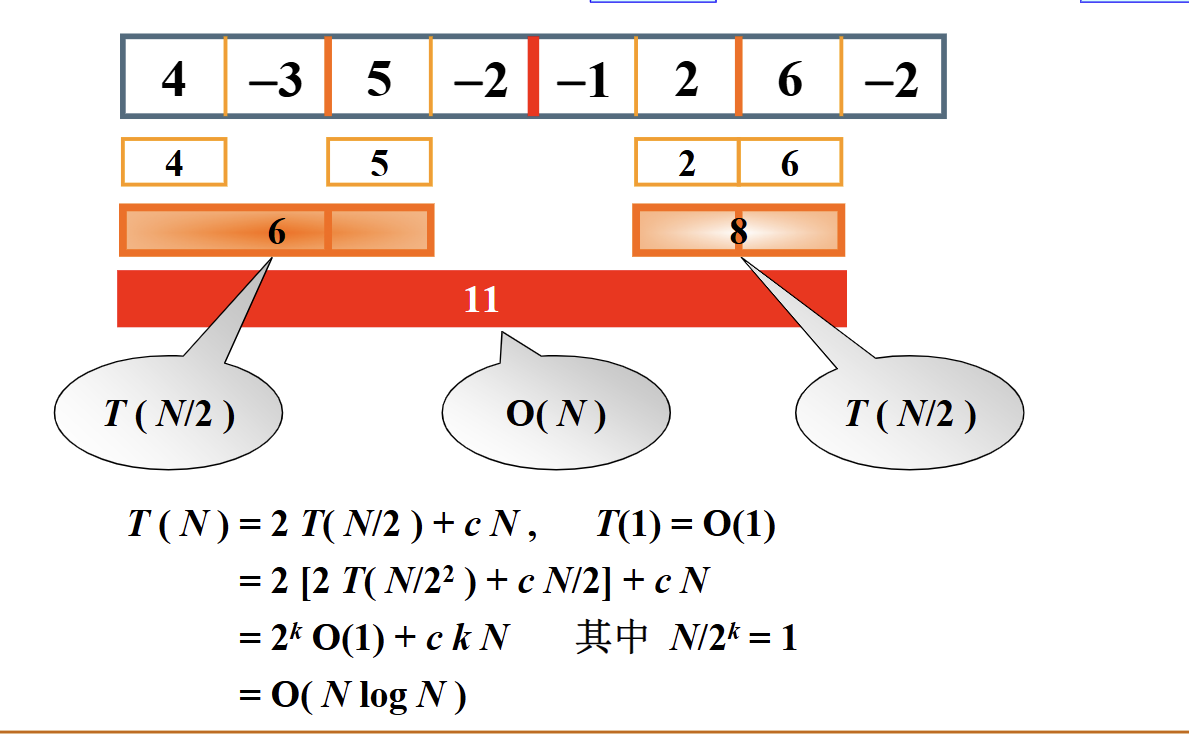
参考：

https://github.com/callmePicacho/Data-Structres/blob/master/README.md

数据结构层次
逻辑结构&存储结构
数据结构组成
关于分治法的时间复杂度证明：
alt text

[SCU练习平台题解]课堂练习

练习
PTA
2024/09/05:
NO1，最大子列和问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;

int Max3(int A,int B,int C)
{
	return A > B ? A > C ? A : C : B > C ? B : C;
}
int DivideAndConquer(int List[],int left ,int right)
{
	int MaxLeftSum,MaxRightSum;
	int MaxLeftBorderSum,MaxRightBorderSum;
	
	int LeftBorderSum,RightBorderSum;
	int center,i;
	
	if(left == right)
	{
		if(List[left] > 0)
		{
			return List[left];
		}else{
			return 0;
		}
	}
	
	center = (left + right) / 2;
	
	MaxLeftSum = DivideAndConquer(List,left,center);
	MaxRightSum = DivideAndConquer(List,center+1,right);
	
	MaxLeftBorderSum = 0,LeftBorderSum = 0;
	for(i = center;i >= left;i --){
		LeftBorderSum += List[i];
		if(LeftBorderSum > MaxLeftBorderSum)
		{
			MaxLeftBorderSum = LeftBorderSum;
		}
	}
	
	MaxRightBorderSum = 0,RightBorderSum = 0;
	for( i = center + 1;i <= right; ++ i)
	{
		RightBorderSum += List[i];
		if(RightBorderSum > MaxRightBorderSum)
		{
			MaxRightBorderSum = RightBorderSum;
		}
	}
	
	return Max3( MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}
int MaxSubseqSum3(int List[],int N)
{
	return DivideAndConquer(List,0,N-1);
}

这题非常经典，分治法当然不是最好的。
“在线算法”实际上是贪心的方法，另一种办法是动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
int dp[100005];
int main()
{
	int t;cin >> t;
	for(int k = 1;k <= t;++ k)
	{
		int n;cin >> n;
		for(int i = 1;i <= n;++ i)cin >> dp[i];
		int start = 1,end = 1,p = 1;
		int maxsum = dp[1];
		for(int i = 2;i <= n;++ i){
			if(dp[i-1] + dp[i] >= dp[i])
				dp[i] = dp[i-1] + dp[i];
			else p = i;
			if(dp[i] > maxsum)
			{
				maxsum = dp[i];start = p;end = i;
			}
		}
		printf("%d\n",maxsum);
	}
	
	
	return 0;
}

但是时间复杂度是O(n*m)肯定会超时，考虑使用单调队列进行优化：

<div class="fold">  <div class="fold-title fold-info collapsed" data-toggle="collapse" href="#collapse-0ad24a9b" role="button" aria-expanded="false" aria-controls="collapse-0ad24a9b">    <div class="fold-arrow">▶</div>动态规划+前缀和+单调队列  </div>  <div class="fold-collapse collapse" id="collapse-0ad24a9b">    <div class="fold-content">      
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
deque<int> dq;
int s[100005];
int main()
{
	int n,m;scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;++ i)scanf("%lld",&s[i]);
	for(int i = 1;i <= n;++ i)s[i] = s[i] + s[i-1];
	int ans = -1e8;
	dq.push_back(0);
	
	for(int i = 1;i <= n;++ i)
	{
		while(!dq.empty()&&dq.front() < i - m)dq.pop_front();
		if(dq.empty())ans = max(ans,s[i]);
		else ans = max(ans,s[i] - s[dq.front()]);
		while(!dq.empty() && s[dq.back()] >= s[i])dq.pop_back();
		dq.push_back(i);
	}
	
	return 0;
}
<p><strong>由此可见，将数据结构与算法结合，威力无穷</strong></p>    </div>  </div></div>

alt text

NO2,多项式的加法和乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include<bits/stdc++.h>
using namespace std;
#define maxn 10010
int a[maxn+1];
int b[maxn+1];
int c[maxn+1];
int d[maxn+1];
void getmul()
{
	int flag = 0;
	for(int i = 0;i <= maxn;++ i)
	{
		if(a[i] != 0)
		{
			for(int j = 0;j <= maxn;++ j)
			{
				if(b[j] != 0)
				{
					d[i+j] += a[i] * b[j];
				}
			}
		}
	}
	int mark = 0;
	for(int i = 0;i <= maxn;++ i)
	{
		if(d[i] != 0)
		{
			mark = i;
			break;
		}
	}
	for(int i = maxn;i >= 0;i --)
	{
		if(d[i] != 0)
		{
			flag = 1;
			cout << d[i] << " " << i << " \n"[i==mark];	
		}
	}
	if(flag == 0)
	{
		cout << "0 0" << endl;
	}
}
void getsum()
{
	int flag = 0;
	for(int i = 0;i <= maxn;++ i)
	{
		c[i] = a[i] + b[i];
	}
	int mark = 0;
	for(int i = 0;i <= maxn;++ i)
	{
		if(c[i] != 0)
		{
			mark = i;
			break;
		}
	}
	for(int i = maxn;i >= 0;i --)
	{
		if(c[i] != 0)
		{
			flag = 1;
			cout << c[i] << " " << i << " \n"[i == mark];	
		}
	}
	if(flag == 0)
	{
		cout << "0 0" << endl;
	}
}
int main()
{
	int num1,num2;
	cin >> num1;
	while(num1--)
	{
		int x,y;
		cin >> x >> y;
		a[y] = x;
	}
	cin >> num2;
	while(num2--)
	{
		int x,y;
		cin >> x >> y;
		b[y] = x;
	}
	getmul();
	getsum();
	
	return 0;
}

4 数组×40044 字节/数组=160176 字节
这大约是 156.5 KB。
这样虽然过了，但是没考虑过空间浪费。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include<bits/stdc++.h>
using namespace std;
#define maxn 10010
typedef struct LNode *List;
struct data{
	int x;
	int y;
};
struct LNode{
	struct data Data[maxn];	
	int Last;
};
List init()
{
	List L = (List)malloc(sizeof(struct LNode));
	L->Last = -1;
	return L;
}
void insert(int x,int y,List L)
{	
	L->Last++;
	L->Data[L->Last].x = x;
	L->Data[L->Last].y = y;
	return ;
}
//int Length(List L){
//	return L->Last+1;
//} 
void getsum(List L1,List L2)
{
	int pointer1 = 0;
	int pointer2 = 0;
	while(pointer1 <= L1->Last && pointer2 <= L2->Last)
	{
		if(L1->Data[pointer1].y > L2->Data[pointer2].y)
		{
			printf("%d %d ",L1->Data[pointer1].x,L1->Data[pointer1].y);
			pointer1++;
		}else if(L1->Data[pointer1].y < L2->Data[pointer2].y)
		{
			printf("%d %d ",L2->Data[pointer2].x,L2->Data[pointer2].y);
			pointer2++;
		}else{
			printf("%d %d ",L1->Data[pointer1].x + L2->Data[pointer2].x,L1->Data[pointer1].y);
			pointer1++;
			pointer2++;
		}
	}
	if(pointer1 <= L1->Last)
	{
		printf("%d %d ",L1->Data[pointer1].x,L1->Data[pointer1].y);
		pointer1++ ;
	}else if(pointer2 <= L2->Last)
	{
		printf("%d %d ",L2->Data[pointer2].x,L2->Data[pointer2].y);
	    pointer2++ ;
	}
}
//void getmul(List L1,List L2)
//{
//	int pointer1 = 0;
//	int pointer2 = 0;
//	for(;pointer1 <= L1->Last;pointer1++ )
//	{
//		for(;pointer2 <= L2->Last;pointer2++ )
//		{
//			
//		}
//	}
//}
int main()
{
	int num1,num2;
	cin >> num1 ;
	List L1 = init();
	while(num1--)
	{
		int x,y;
		cin >> x >> y;
		insert(x,y,L1);
	}
	cin >> num2;
	List L2 = init();
	while(num2--)
	{
		int x,y;
		cin >> x >> y;
		insert(x,y,L2);
	}
//	for(int i=0;i<Length(L1);i++)
//		printf("%d %d ",L1->Data[i].x,L1->Data[i].y);
//	printf("\n");
//	for(int i=0;i<Length(L2);i++)
//		printf("%d %d ",L2->Data[i].x,L2->Data[i].y);
	printf("\n");
	getsum(L1,L2);
//	getmul();
	
	return 0;
}

这段中尝试使用了动态数组实现顺序表的办法，完成了多项式加法

  • 优势：相比上一份静态数组，处理数据时拿多少用多少。比如同样一组输入，空间占用从165kB降至不到100B。
  • 缺点：虽然实现，但是代码中有几个问题：
  • 1.在线算法，算一条输出一条，不灵活，这也解释了为什么乘法部分没有继续写。更好的做法是再开一个数组存答案。
  • 2.输出部分未封装，题目部分有格式要求，较复杂的输出适合单独封装一个函数做输出。
  • 3.空间连续，这是开数组和开链表的重要区别：数组空间必须物理上连续，而实际上计算机内存物理上并不连续，你以为的连续实际上是操作系统给出的抽象层，造成了空间连续的假象（逻辑上连续），这就会在要求比较苛刻的情况中浪费空间。

Tips：看懂一份代码不难，重要的是如何独立写出来。一个好办法是阅读注释，注释和编写过程中的调试遗迹是好东西，编写边调试即可化难为简。
可惜的是，大多数题解将调试遗迹删去。

最优解法：链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include<stdio.h>
#include<stdlib.h>
typedef struct Node *List;
struct Node{
	List Next;
	int z;   // 指数 
	int x;  // 系数 
};

// 读入链表 
List Read(){
	List L = (List)malloc(sizeof(struct Node));
	List head = L;
	int n;
	int i=0;
	scanf("%d",&n);
	for(i=0;i<n;i++){
		int x;
		int z;
		List t = (List)malloc(sizeof(struct Node));
		scanf("%d %d",&x,&z);
		t->x = x;
		t->z = z;
		L->Next = t;
		L = L->Next;
	}
	L->Next = NULL;
	return head->Next;
}

// 实现加法运算 
List addition(List L1,List L2){
	List tmpL1 = L1;
	List tmpL2 = L2;
	List add=(List)malloc(sizeof(struct Node));
	add->Next = NULL;
	List head = add;
	List t;
	while(tmpL1 && tmpL2){
		t = (List)malloc(sizeof(struct Node));
		if(tmpL1->z == tmpL2->z){  //指数相等，系数相加  
			t->x = tmpL1->x + tmpL2->x;
			t->z = tmpL1->z;
			tmpL1 = tmpL1->Next;
			tmpL2 = tmpL2->Next;
		}else if(tmpL1->z < tmpL2->z){   // L2 结点指数更大，把 L2 结点加入链表 
			t->x = tmpL2->x;
			t->z = tmpL2->z;
			tmpL2 = tmpL2->Next;
		}else if(tmpL2->z < tmpL1->z){   // L1 结点指数更大，把 L1 结点加入链表 
			t->x = tmpL1->x;
			t->z = tmpL1->z;
			tmpL1 = tmpL1->Next;
		}
		add->Next = t;
		add = add->Next; 
	}
	if(tmpL1)   // 若 L1 不等于 NULL，将剩下结点加入其后 
		add->Next = tmpL1;
	else if(tmpL2)  // 同理 
		add->Next = tmpL2;
	return head->Next; // head 结点只有指针域存值 
}

// 实现乘法运算 
List multiplication(List L1,List L2){
	List tmpL1 = L1;
	List tmpL2 = L2;
	List mul=(List)malloc(sizeof(struct Node));
	mul->Next = NULL;
	List head = mul;
	List t;
	for(;tmpL1;tmpL1=tmpL1->Next)
		for(tmpL2 = L2;tmpL2;tmpL2=tmpL2->Next){
			t = (List)malloc(sizeof(struct Node));
			t->x = tmpL1->x * tmpL2->x;  // 系数相乘
			t->z = tmpL1->z + tmpL2->z;  // 指数相加
			t->Next = NULL;
			head = addition(t,mul);  // 将新增结点和之前已经排好序的结点排序 
			mul = head; // 重新确定开头 
		}
	return head;
}
void Print(List L){
	List t = L;
	int flag = 1;
	for(;t;t = t->Next){
		if(!flag && t->x)   //控制空格输出
			printf(" ");
		if(t->x){   // 如果系数为 0，不输出 
			printf("%d %d",t->x,t->z);
			flag =0;		
		}
	}
	if(flag)
		printf("0 0");
	printf("\n");
}
int main(){
	List L1,L2,add,mul;
	L1 = Read();
	L2 = Read();
	add = addition(L1,L2);
	mul = multiplication(L1,L2);
	Print(mul);
	Print(add);
	return 0;
}

0908
NO3,树的同构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<iostream>
#include<malloc.h>
#define null -1
using namespace std;
struct TreeNode{
	char data;    // 存值 
	int left;   // 左子树的下标 
	int right;  // 右子树的下标 
}T1[10],T2[10];
// 返回根结点 
int create(struct TreeNode T[]){
	int n;
	int root = 0;
	char left,right;
	cin>>n;
	if(!n)
		return null;
	for(int i=0;i<n;i++){
		cin>>T[i].data>>left>>right;
		if(left=='-')
			T[i].left = null;
		else{
			T[i].left = left-'0';
			root -= T[i].left;
		}
		if(right=='-')
			T[i].right = null;
		else{
			T[i].right = right-'0';
			root -= T[i].right;
		}
		// 0 累加到 n-1 
		root +=i;	
	}
	return root;
}
// 判断是否同构
bool judge(int R1,int R2){
	if(R1 == null && R2 == null)   // 都为空 
		return true;
	if(R1 == null && R2 != null || R1 != null && R2 == null)    // 一个为空，一个不为空
		return false;
	if(T1[R1].data != T2[R2].data)   // 值不同
		return false;
	if((T1[R1].left != null && T2[R2].left != null )&&(T1[T1[R1].left].data == T2[T2[R2].left].data))  // 左儿子不为空且值相等
		return judge(T1[R1].left,T2[R2].left) && judge(T1[R1].right,T2[R2].right);
	else   // 左儿子不为空且值不等  或者 某一个左儿子为空 
		return judge(T1[R1].right,T2[R2].left) && judge(T1[R1].left,T2[R2].right);
} 
int main(){
	int R1,R2;
	R1 = create(T1);
	R2 = create(T2);
	if(judge(R1,R2))
		cout<<"Yes";
	else
		cout<<"No";
	return 0;
}

之后的笔记就是关于大二下左老师算法设计课程。

Week2:

之前讲了完整的时间复杂度分析理论。这节课承接上文：
算法分析中常用的函数：

  • 幂函数
  • 取整函数
  • 多项式函数
  • 指数函数

我们现代的普通计算机计算能力是每秒1亿次，10^9，当一个问题的计算规模超过10^13，一万亿次时，我们认为一般是不可接受的。
拿斐波那契数列问题举例，2^40接近10^13，O(2^n)的算法时间复杂度对于我们只能算到40项。
而我们手算时间复杂度是O(n)的
通过快速幂方法结合矩阵乘法，这个问题可以使用O(logn)的算法程序来解决，这样计算10^13的问题只需要计算40次，反过来了。
这个例子非常典型，展现了时间复杂度优化对于解决问题的重要性。

要理解为什么排序问题的最优时间复杂度是 ( \Omega(n \log n) )，我们需要考虑基于比较的排序算法的性质。基于比较的排序算法是那些仅通过比较元素来确定它们的顺序的算法。这些算法的最优时间复杂度由决策树模型来确定。

逐步解释：

  1. 决策树模型：

    • 在决策树模型中，每个内部节点代表两个元素之间的比较，每个叶节点代表可能的排序结果。
    • 对于 ( n ) 个元素，有 ( n! )（n的阶乘）种可能的排列。因此，决策树必须至少有 ( n! ) 个叶节点。

  2. 树的高度：

    • 二叉树的高度是最大的路径长度从根到叶。在决策树中，高度代表最坏情况下的比较次数。
    • 一个有 ( n! ) 个叶节点的二叉树的高度至少是 ( \log_2(n!) )。

  3. 斯特林近似：

    • 斯特林近似表明 ( n! \approx \sqrt{2 \pi n} \left( \frac{n}{e} \right)^n )。
    • 使用这个近似，我们可以估计 ( \log_2(n!) \approx \log_2 \left( \sqrt{2 \pi n} \left( \frac{n}{e} \right)^n \right) )。

  4. 简化对数：

    • ( \log_2(n!) \approx \log_2 \left( \sqrt{2 \pi n} \right) + \log_2 \left( \left( \frac{n}{e} \right)^n \right) )
    • ( \log_2(n!) \approx \frac{1}{2} \log_2(2 \pi n) + n \log_2 \left( \frac{n}{e} \right) )
    • ( \log_2(n!) \approx \frac{1}{2} \log_2(2 \pi n) + n \log_2(n) - n \log_2(e) )

  5. 主导项：

    • 当 ( n ) 变得很大时，项 ( n \log_2(n) ) 主导表达式。
    • 因此，( \log_2(n!) \approx n \log_2(n) )。

  6. 结论：

    • 由于决策树的高度至少是 ( \log_2(n!) )，并且 ( \log_2(n!) \approx n \log_2(n) )，任何基于比较的排序算法在最坏情况下的比较次数至少是 ( n \log_2(n) )。
    • 这意味着基于比较的排序算法的最优时间复杂度是 ( \Omega(n \log n) )。

之后还讲了递归算法的时间复杂度分析。

“这块东西你们其实以前也见过了，但是没有经过一个系统的学习，产生一个本质的了解。通过这两节课让大家对这个有一个本质的了解。”

递归与其说是一种算法，不如说是一种思维方式。（与数学归纳法类似的想法）
递归的核心要素：自己定义自己——自己调用自己
之后老师从头分析了递归编程解决排列组合问题的每一个细节。
指出设计递归程序的思维方式转变：自顶向下

Week3:

Week4:

Week5:

Week6:

Week7:

Week8:

Week9:

Week10:

Week11:

Week12:

Week13:

Week14:

Week15:

Week16:

Theory > 数据结构与算法 & 算法设计
数据结构与算法
https://43.242.201.154/2024/09/05/Algorithms & Datastructures/
Author
Dong
Posted on
September 5, 2024
Licensed under