信息安全数学基础-第二章-同余

“同余”是大自然的循环现象，是一种等价关系，研究同余的优点在于:化无限为有限。

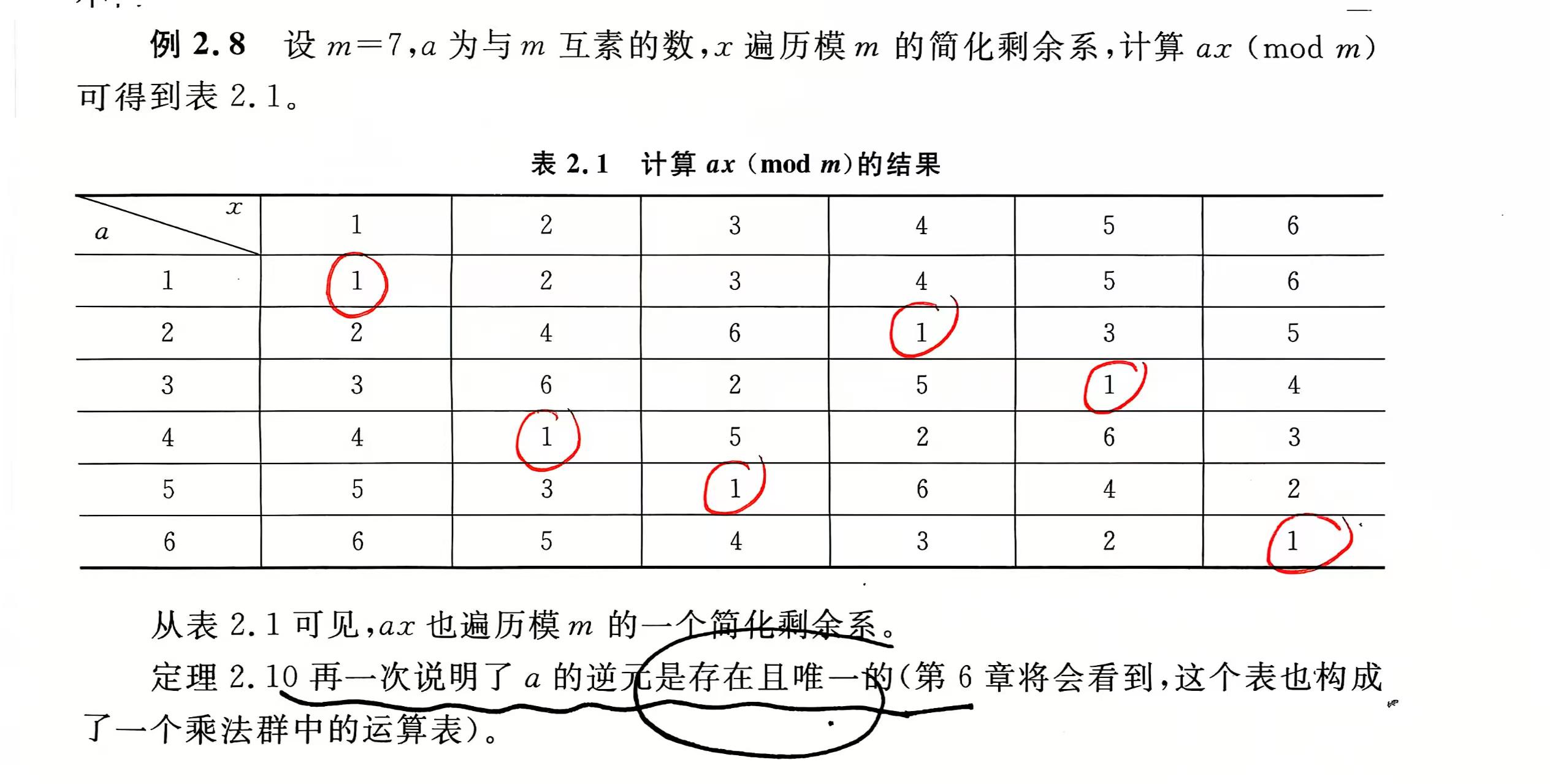
图中每一列中的元素以相似的方式不重不漏地出现，这种规律就是剩余类。同余这种等价关系——它将整数划分成了n-1在模n意义下的等价类——n的完全剩余系。
全体整数按照模m是否同余划分成若干两两不相交的集合，使得每一个集合中的任意两个整数模m一定同余，而不属于同一集合的任意两个整数模m不同余。

Abstract：

• 模运算的基本性质
• 剩余类：将所有整数按照模m划分成了不同的类
• 完全剩余系：从每个剩余类中拿一个出来组成完全剩余系
• 简化剩余类：是m的完全剩余系中与m互素的数构成的子集
• 简化剩余系：从每个简化剩余类中拿一个出来组成简化剩余系
• 欧拉定理
• Wilson定理
• 费马定理

考点0：模运算的基本性质

考点1：同余等价关系定义、三大性质（自反、对称、传递）

同余的定义：

同余的充要条件：

同余的基本性质：

由此可以说明同余是一种等价关系（离散数学-二元关系）。

考点2：利用乘法（降幂）计算较大数的mod运算

实质是利用同余的乘性。

考点3：验算大整数乘法结果（模9法，弃9法）

定理基础：

推论应用：

推论应用(模7/11/13)：

例题：

考点4：欧拉函数的定义以及利用标准因数分解式计算欧拉函数

定义：

设m是一个正整数，则m个整数0,1,…，m-1中与m互素的整数的个数，记为$\phi(m)$，叫做欧拉函数。

欧拉函数只有在互素的情况下才有乘性！

考点5：费马小定理、威尔逊定理、欧拉定理