信息安全数学基础-第一章-整除
在整数集合中,整除是一种重要的二元关系。这些概念与性质又是整数集合中另一种重要的二元关系——同余关系的基础。
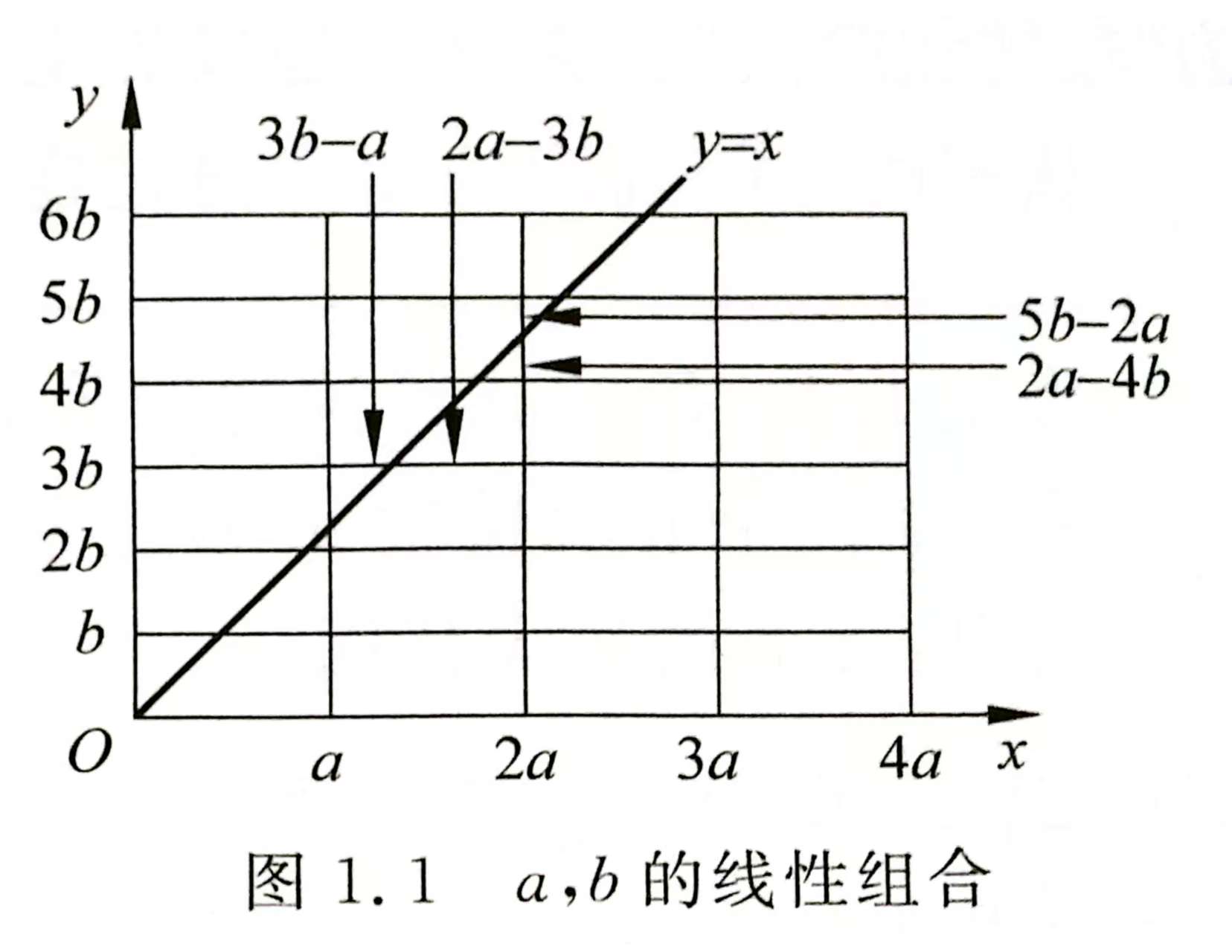
因此,(a,b)也可以视为利用长度为a和b的两把“尺子”可以“丈量”的最小长度。
Abstract:
- 判断素数问题,定理1.4对应到了O(√n)算法优化方法的证明
- 素数筛的两种方法:埃氏筛和欧拉筛,刚好对应了两种素数不可穷举的证明思想
- 辗转相除法及其证明
- 贝祖定理,扩展欧几里得算法的应用——求逆元
- 素数的性质,最大公因数和最小公倍数
- 算术基本定理
重要定理及证明(素数部分)
定理1.3:
- 设a,b,c!=0是三个正整数。若c|a,c|b,则对任意整数s,t有
- c | sa+tb
这条定理通过整除定义证明即可。但是这条定理也值得记下,它提供了后边欧几里得除法的证明方式,而扩展欧几里得除法提供了求逆元的方法,这又是后续RSA加密算法的关键环节,所以说这条定理差不多算是大楼的第一块砖了,基础却重要。
定理1.4
- 设n是一个正合数,p是n的一个大于1的最小正因数,则p一定是素数,且p小于等于√n。
这条定理应该是整除部分最重要的之一了。- 空口无凭,举个实际应用的例子-判断一个数是否是素数:
“非正式地说,这条定理说明了两点:素数可以视为合数的“组成部分”,且这一“组成成分”中必然有一部分小于√n”
1 | |
为什么只枚举到√n?,这里就用到了定理1.4,大大提高了算法时间复杂度。
值得说明的是,对于判断素数问题,O(√n)即是速度瓶颈,也就是说这基本上是最快的方法了。
定理1.5
素数有无穷多个
课上讲了两种证明方法,思考发现,两种证明思想刚刚好对应了两种编程算法,这里先介绍证明方法:
证明A:

证明B:

算法设计
对于寻找范围内所有素数的问题,网上资料会说:欧拉筛是埃氏筛法的优化、欧拉筛和埃氏筛的本质都一样:“素数的倍数不是素数。”、欧拉筛避免了埃氏筛中重复筛选的问题、等等.
这些说法都不错,但是当我们学过算法的数学理论,不难发现这两种算法其实是两种不同证明思想的体现,而不是简单的算法优化与继承。
埃氏筛法对应证法A,欧拉筛对应证法B
Eraosthenes(埃拉托斯尼筛法)埃氏筛法
时间复杂度O(nloglogn)
1 | |
埃氏筛法的相关证明
证明从i平方开始枚举可行

证明埃氏筛正确,并证明它无法避免重复筛选
假设存在一个数n,它是i的倍数但大于i^2,且n还没有被任何小于i的质数筛去。那么n可以表示为n = i * k,其中k > i。
如果k是质数:
那么k一定大于i(因为k是n的因子且n > i^2),那么k*i > i^2,那么当前i一定可以筛掉这个n,合理。如果k是合数:
且都是素数
那么根据定理1.23(算术基本定理),任意整数可以唯一的表示成:那么之前遍历过的素数一定筛掉了当前的n,合理。
综上所述,埃氏筛可以实现不漏的筛选。
无法避免重复?,里边有几个素数,n就被重复筛了多少次。由此,每个数被重复筛掉过次数也可以知道了。
证明是可以缩小i的枚举范围至√maxn,回答优化后的算法时间复杂度。
- 证明就是定理1.4,无需再枚举大于√maxn的素数,因为正合数n的最小正因数一定小于√n,且为素数。
这也是手算的重要技巧,被老师在课堂重点强调: ▶编程测试**调用计时函数,计算1000以内的素数1000次,记录运行时间**
▶编程测试**调用计时函数,计算1000以内的素数1000次,记录运行时间**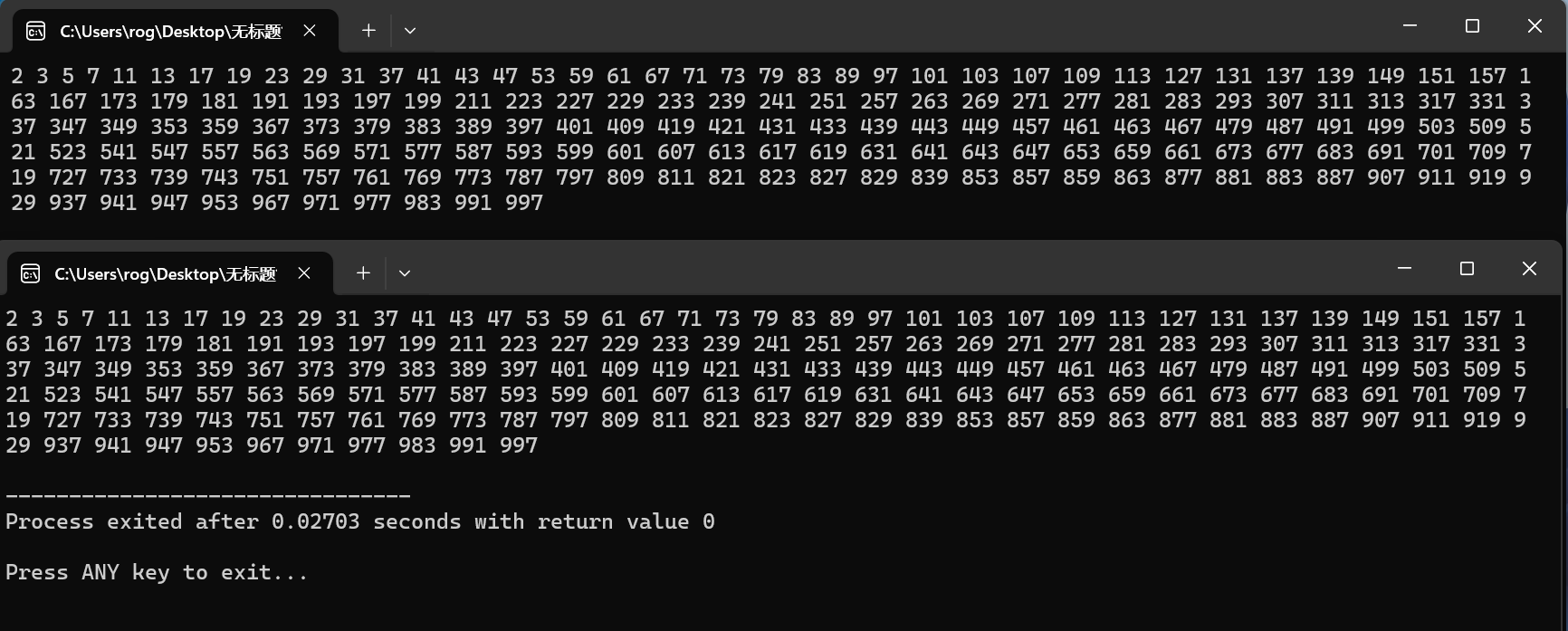
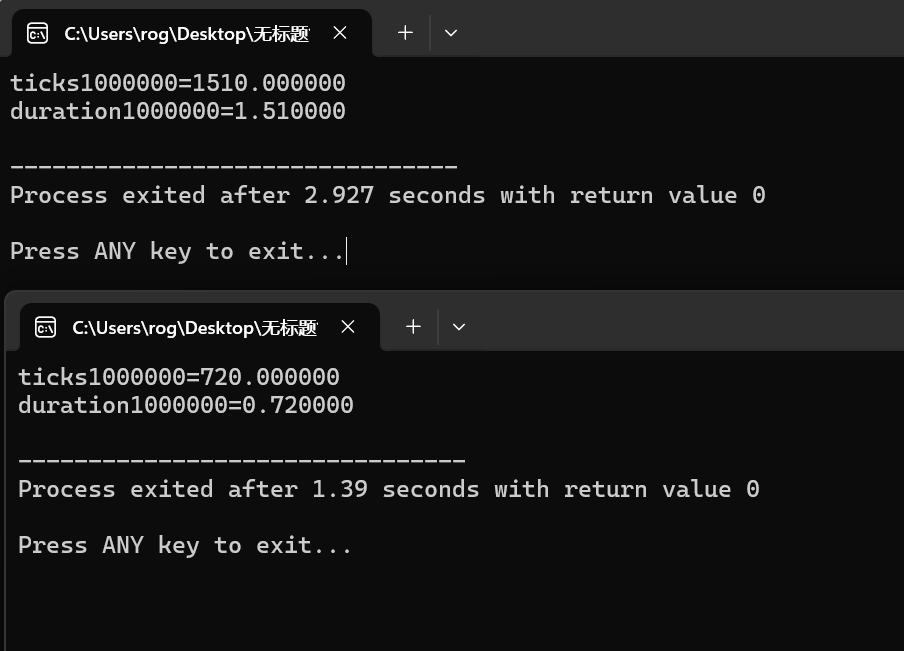
可以看到,优化后的埃氏筛法快了近一倍!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3;
bool isprime[maxn+10];
typedef long long int ull;
clock_t start,endd;
double duration;
int Test = 1000;
void seive(){
memset(isprime,true,sizeof(isprime));
isprime[0]=isprime[1]=false;
for(ull i=2;i<=maxn;i++){
// if(i >= sqrt(maxn))break;
if (isprime[i]) {
for (ull j = i * i; j <= maxn; j += i) {//枚举倍数并筛去
isprime[j] = false;
}
}
}
}
int main()
{
// start = clock();
// for(int i = 0;i < Test;++ i)
// {
seive();
// }
// endd = clock();
for(int i = 0;i < maxn;++i)
{
if(isprime[i])
{
cout << i << " ";
}
}
cout << endl;
// printf("ticks%d=%f\n",maxn,(double)(endd-start));
// duration = ((double)(endd-start))/CLK_TCK;
// printf("duration%d=%lf\n",maxn,duration);
return 0;
}
欧拉筛
时间复杂度:O(n)
1 | |
补充定理:

课堂思考题及证明:

重要定理及证明(gcd部分)
良序原理
自然数集的每个非空子集都有个最小元素。也称最小数原理。
定理1.8(贝祖定理):
这是GCD 的另一个定义,在高等数学中很有帮助,尤其是环论。
推论:
- a 和 b 的任何公约数也会被GCD整除。
- 三个或更多数字的 GCD 等于所有数字的质因数的乘积
- 计算两个整数的 GCD 的 Euclid 算法足以计算任意多个整数的 GCD。
定理1.9:

只有两个数互素的时候才有乘法逆元
定理1.12:
欧几里得定理:
欧几里得除法:
基本定义与证明

于是由欧几里得定理,(a,b) = (r0,r1) = (r1,r2) = …… = (rn,0) = rn
即gcd(a,b)=gcd(b,a%b)
扩展的欧几里得算法
GCD 可以表示为两个原始数字的线性组合,即两个数字之和,每个数字乘以一个整数(例如,21 = 5 × 105 + (−2) × 252)。
GCD 总是可以用这种方式表达的事实被称为 Bézout 贝祖恒等式。
定理1.13:

证明
核心:核心思想是反复构造并求解一系列适于裴蜀定理(贝祖定理)的恒等式,进而得到s和t
书P12-13:”以q为纽带,尝试计算s和t的数列。通过尝试和整理,得到定理。”
但是书上并没有说明s和t的数列是怎么找到的,这里将整个证明过程补全。
一切都从贝祖恒等式开始:
那么现在只需证明:
数学归纳法:
算法设计
区别与联系
- 欧几里得算法,即辗转相除法,将求两个较大数的公因数转化为求两个较小数的公因数。
- 扩展欧几里得算法,引入了关于s和t的递推关系,在计算r的递推关系求出(a,b)的同时,算出s和t
- 扩展欧几里得算法求逆元,是扩展欧几里得算法的主要应用
由定理1.9可知,当(m,b)=1时,sm+tb=(m,b)=1,因此,tb=1(mod m)
于是找到了t,这是b在乘法群中的乘法逆元(第六章)
欧几里得算法
1 | |
扩展欧几里得算法
1 | |
扩展欧几里得算法求逆元
1 | |
补充定理:
这部能够深化对素数和gcd的认识,提出了一些实用的性质。
同时又像是贝祖定理的拓展(因为所有证明都离不开贝祖定理)
在这对它们进行整理。
互素的充要条件:

最大公因数的充要条件


最大公因数的性质

互素的gcd性质

推论1:
设a,b,c是三个整数,且c!=0,如果c|ab,(a,c)=1,则c|b
推论2:
设p是素数, 若p|ab, 则p|a或p|b.
推论3:
设a,b,c是整数,若(a,c)=1,(b,c)=1,则(ab,c)=1
推论4:
设a1,a2,……,an是整数,p是素数,p|a1a2……an,则p|某个a。
小结
证明方法略,贝祖定理和反证法即可完成所有。
这部分也是这节课主要理解难度所在,看起来杂乱繁琐,但是形散而神不散。
概括:一个数被拆成乘积形式,素数是其基本组成部分。
- 发现了吗,这个规律就是下一部分的算术基本定理!!!
理解到位,很自然地就过渡到了下一部分,到此为止这章内容的线索也就很明显了。
思考题及其证明
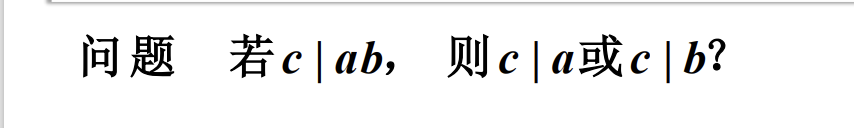
分类讨论:
若c是素数,由推论2,ab必然有一个被c整除。
若c非素数,举个反例,12=3*4,6|12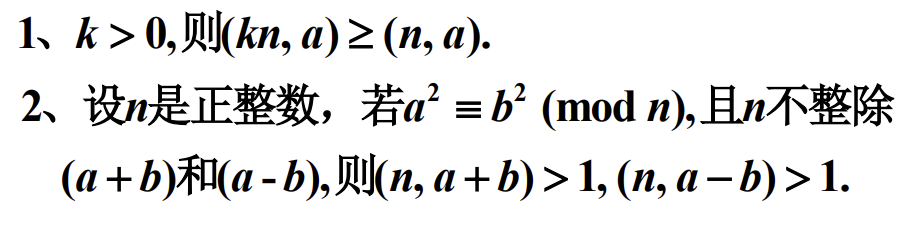
1.根据gcd性质,公因数一定小于等于最大公因数
2.由题:n|(a+b)(a-b),那么由推论1反证即可。
1.根据有理数的性质:有理数可以被表示成分数,构造即可。
2.由上述互素的gcd性质可以知道:
那么结合最大公因数的性质(图中框出的那条),即可得证。
重要定理及证明(lcm部分)

定理1.19:
设a,b是两个互素的正整数,则:
(1)
(2)

定理1.20:
(1)
(2)

算术基本定理:

标准分解式:

标准分解式的应用:
判断整除

求因数个数

求gcd和lcm

综合应用与总结:
找了半天一年前的博客笔记,但是再也找不到了,有一些失落。
但还记得,那是梦开始的地方,如今时隔一年了,问题终于有了答案。
翻到了当时讨论出的AC代码:
1 | |
什么意思呢?公式两边除以n平方,那么根据这条定理:
只需要枚举找到这两个互素的数就可以找到a,b了,大大减少了循环次数,是不是很神奇。
The End.
参考资料:
王鑫教授的课件
《信息安全数学基础》(任伟)
维基百科-欧几里得算法
OI选手现充|junyu33博客